Odds and Ends

The Dinneen Graph?

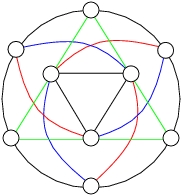
The graph displayed in the icon for this page is the smallest non-partition graph (and only one with 9 vertices) that satisfies the triangle condition which contradicts a conjecture by D. DeTemple, F. Harray and J. Robertson. More information may be found in the paper (my first in experimental / theoretical graph theory!) listed below. Duane W. DeTemple, Michael J. Dinneen, Kevin L. McAvaney and Jack M. Robertson, ``Recent examples in the theory of partition graphs,'' Discrete Mathematics, volume 113, pages 255-258, 1993.

A Computational Attack on the Conjectures of Graffiti: New Counterexamples and Proofs

One of the difficulties of obtaining a new result in graph theory has been finding the statement of the result. This situation may soon change as computers are now capable of generating interesting mathematical conjectures. A conjecture generating program, called Graffiti, was developed by Siemion Fajtlowicz in 1986 at the University of Houston, Texas. It uses a database of graphs and heuristically checks for relationships among certain graph invariants. The main task of the program is to decide which of these relationships should be accepted as conjectures.

Having obtained a readily available computer tape of all the nonisomorphic graphs with 10 or fewer vertices, we have tested over 200 of the Graffiti conjectures and have found counterexamples for several of them (and a few proofs). Our Graffiti research is summerized in the following two papers.

Tony L. Brewster and Michael J. Dinneen and Vance Faber, ``A Computational Attack on the Conjectures of Graffiti: New Counterexamples and Proofs'' , Discrete Mathematics, 147(1-3):35--55, 1995.

Michael J. Dinneen, ``A Computational Attack on Graffiti's Matching and Chromatic Number Conjectures'' , Los Alamos National Laboratory manuscript (1992).

For related papers on the conjectures of Graffiti see Ermelinda DeLaVina's Graffiti page.

My two cents in unconventional models of computation

Michael J. Dinneen, ``VLSI Layouts and DNA Physical Mappings'' , Los Alamos LACES 05C-95-20 (http://arxiv.org/abs/math/9503221).

Cristian S. Calude, Michael J. Dinneen and Karl Svozil. ``Reflections on Quantum Computing'' , Complexity, Vol 6(1), p35-37, 2000.

Joshua J. Arulanandham, Cristian S. Calude, and Michael J. Dinneen. ``Bead--Sort: A Natural Sorting Algorithm'' , Bulletin of the E.A.T.C.S., Vol 76, 153--162, 2002.

Joshua J. Arulanandham, Cristian S. Calude, and Michael J. Dinneen. ``A Fast Natural Algorithm for Searching'' , Theoretical Computer Science 320, 1, 3--13, 2004.

Joshua J. Arulanandham, Cristian S. Calude and Michael J. Dinneen" ``Balance Machines: Computing = Balancing", in "Aspects of Molecular Computing" published in the Natural Computing Springer Series (N. Jonoska, Gh. Paun, G. Rozenberg editors), LNCS Vol 2933, pages 36--47, Nov 2003.

Joshua J. Arulanandham and Michael J. Dinneen ``Balance machines: A new formalism for computing'', Report {CDMTCS}-256, Centre for Discrete Mathematics and Theoretical Computer Science, University of Auckland, Auckland, New Zealand, December 2004.

Michael J. Dinneen, Yun-Bum Kim and Radu Nicolescu}, ``New Solutions to the Firing Squad Synchronization Problem for Neural and Hyperdag P Systems}'', Membrane Computing and Biologically Inspired Process Calculi, Third Workshop, MeCBIC 2009, Bologna, Italy, September 5, 2009}, pages 117-130, 2009.

Radu Nicolescu, Michael J. Dinneen and Yun-Bum Kim, ``Discovering the Membrane Topology of Hyperdag P Systems'', Revised Selected and Invited papers of 10th International Workshop on Membrane Computing, (WMC 2009), Curtea~de~Arge\c{s}, Romania}, Lecture Notes in Computer Science, volume 5957, pages 410-435, 2010.

We were the first to compute some exact bits of an Omega number.

Cristian S. Calude, Michael J. Dinneen and Chi-Kou Shu. Computing a Glimpse of Randomness. In Experimental Mathematics 11:2, 369-378, 2002.

Cristian S. Calude and Michael J. Dinneen. Exact Approximations of Omega Numbers. To appear in Int. J. of Bifurcation & Chaos}, Vol. 17, 2007.

And finally some other topics:

Michael J. Dinneen and Bakh Khoussainov, ``Automata with Equational Constraints'' , Report CDMTCS-111 (1999).

C.S. Calude, E. Calude and M.J. Dinneen, ``What is the Value of Taxicab(6)?'', JUCS 10(9), pages 1196-1203, Oct 2003.

C.S. Calude, E. Calude and M.J. Dinneen, ``A New Measure of the Difficulty of Problems'', J. of Mult.-Valued Logic & Soft. Computing, Vol 12., pp. 285-307, 2006.

David H. Bailey, Jonathan M. Borwein, Cristian S. Calude, Michael J. Dinneen, Monica Dumitrescu & Alex Yee: An Empirical Approach to the Normality of Pi, Experimental Mathematics, 21:4, 375-384, 2012