Texture Analysis: an Overview

Texture analysis concerns mainly with feature extraction and image coding. Feature extraction identifies and selects a set of distinguishing and sufficient features to characterise a texture. Image coding derives a compact texture description from selected features. By representing a complex texture with a small number of measurable features or parameters, texture analysis archives great dimension-reduction and enables automated texture processing

Many texture analysis methods have been proposed in the past several decades. The available methods might be categorised into geometrical, statistical, model-based and signal processing methods [98], but many methods apparently stride over more than one above category. For instance, an MGRF model derives a joint probability distribution on statistical image features for texture description, which could be in both model-based and statistical categories.

This thesis rather considers two more general categories, namely, descriptive and generic approaches. A descriptive approach describes a texture by a set of selected features, which provides a simple summary about which features are in the texture. As a result, a texture is represented by a specific signature that is distinguished from the signatures extracted from other textures. A generic approach makes further inferences from observed image features from a texture, which derives a more generic mathematical model to encapsulate available knowledge and observations about the texture. In other words, the generic approach attempts to reach conclusions that extend beyond the simple description of the observation as in the descriptive approach. In a model a texture is usually characterised by model parameters.

The difference is that the descriptive approach only describes the sample, but the genric/inferential approach infers the property of the entire population based on observations from the sample. Such a categorisation is conceptually similar to the categorisation of descriptive versus inferential statistics. So, the descriptive approach is more useful for discriminating different texture samples, while the generic approach provides better understanding of texture and is also useful in synthesising textures.

Descriptive Approach

A descriptive approach derives a quantitative description of a texture in terms of a manageable set of feature measures.

Let $\mathbf{F} =\{\mathbf{F}_i:i=1..n\}$ denote a set of $n$ texture features. A texture is quantified by a vector of feature measures $\mathbf{f} =\{\mathbf{f}_i:i=1..n\}$, where $\mathbf{f}_i$ represents a measure of the feature $\mathbf{F}_i$. Each feature measure is a scalar value indicating the degree to which the corresponding feature is present in the texture. All the features constitute a $n$-dimensional feature space in which a texture is represented by an empirical distribution on features, i.e. a histogram with $n$ bins. In such a way, a descriptive approach formulate textures in a metric space that allows to apply various quantitative analysis techniques in obtaining efficient solutions to the problem of texture recognition, classification and segmentation.

It is important for a descriptive approach to select an appropriate set of features, i.e. to determine which and how many features should be included into the set. A too small feature space might result in insufficient representation, but too large the dimensionality leads to computational difficulty, i.e. if the space dimensionality exceeds $20-25$, the clustering suffers from so-called ``curse of dimensionality''. In addition, the possible interference between features should also be controlled to achieve effective representation. It is still a profoundly difficult challenge to find a set of optimal and sufficient features being both universally accurate and effective for describing various textures.

By different techniques involved in feature extraction, descriptive approaches can be further divided into statistical and spectral methods.

Statistical methods

collect image signal statistics from the spatial domain as feature descriptors. Commonly applied statistics include 1D histograms, moments, grey-level co-occurrence matrixes, and etc. Usually lower-order image statistics, particularly first- and second-order statistics, are exploited in texture analysis. First-order statistics, such as the mean, standard deviation and higher-order moments of the histogram, concern with properties of individual pixels. Second-order statistics also account for the spatial inter-dependency or co-occurrence of two pixels at specific relative positions. Grey level co-occurrence matrices (GLCM) [44], grey level differences [105], autocorrelation function, and local binary pattern operator [79] are the most popular second-order statistics for texture description. Higher than second-order statistical features have also been investigated [33,96], but the computational complexity increases exponentially with the order of statistics.

The Haralick features [44], derived from the GLCM, are one of the most popular feature set. Also known as the grey-level spatial dependence matrix, the GLCM accounts for the spatial relationship of each pixel pair in the image. Each element $GLCM_{(\delta_{x},\delta_{y})}(i,j)$ of the matrix represents an estimate of the probability of the co-occurrence of grey levels $i$ and $j$ at two arbitrary locations separated by the displacement $(\delta_{x},\delta_{y})$.

Initially, Haralick features include angular second moment, contrast, correlation, variance, inverse second difference moment, and etc [44]. Each of these statistics is related to a certain image feature. For instance, the statistic `angular second moment' measures the closeness of distribution in the GLCM to the GLCM diagonal, which is related to homogeneity of an image. The statistic `contrast' measures the amount of local variations in an image. The statistic `correlation' measures the joint probability of co-occurrence of certain pixel pairs.

Spectral methods

refer to the frequency domain where features are related to statistics of filter responses. Evidence shows that a tuned bandpass filter bank resembles the structure of the neural receptive fields in the human visual system [57,21]. This is the main motivation of spectral methods to extend feature extraction into the spatial frequency domain. Feature extraction in spatial frequency domain has several advantages. First, a filter is selective, i.e. it enhances only certain features while suppresses others. For instance, Laplacian and Laplacian of Gaussian (LOG) filters are usually good edge detectors, while low-pass Gaussian filters are useful for blob detection. Second, the periodicity structure of a texture can be represented explicitly in a certain spatial frequency in the spectral domain.

Spectral methods usually use filter banks [63,71,100,101,102] or image pyramids [46,22] to convert an image from the spatial domain into the frequency domain and vice-versa.

A filter bank consists of a range of parallel filters, each filter being tuned to a particular spatial frequency, orientation or scale. Like in statistical methods, the distribution of feature measures (e.g., wavelength coefficient for a wavelet transform) provides a sparse texture description which can be used directly as input to further classification or segmentation. However, the resulting description is over-complete, because it contains an increase and thus redundancy in information content [16].

Formally, a linear filter corresponds to an invertible linear transform, characterised by a set of basis and projection functions [12]. A filtering operation decomposes an image ${g}$ into a weighted sum of basis functions $\mathbf{b}=\{\mathbf{b}_i: i=1..n\}$,

$${g} = \sum_{i}^{n}\mathbf{c}_i\cdot {\mathbf{b}}_i ,$$

Here $\mathbf{c}=\{\mathbf{c}_i: i=1..n\}$ are the transformation coefficients, which are computed using the projection functions $\mathbf{p}=\{\mathbf{p}_i: i=1..n\}$ as follows,

$$\mathbf{c}_i = \mathbf{p}_i\cdot {{g}}$$

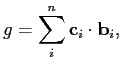
Two-dimensional Gabor filters have been widely used in constructing filter bank [51]. A Gabor filter is a linear, local filter that has its impulse response like a cosine modulated by a gaussian envelope [32]. Each Gabor filter is characterised by an orientation or spatial frequency, which generates the Gabor convolution energy measure of an image. Gabor filters are particularly efficient in detecting the frequency channels and orientations of texture pattern with high precision [74]. Figure 5.1 visualises the filtering responses of a texture produced by a bank of simple Gabor filters.

A few spectral methods have been proposed recently. For example, Leung and Malik identify textons (the cluster centres), as feature descriptors, from filter responses of a stack of training images, and then apply a $k-NN$ classifier for material classification [62,63]. Also, Konishi and Yuille proposed a Bayesian classifier based on the joint probability distribution of filter responses [56].

Spectral methods have a few ill-posed problems. For instance, the selection of filters is mostly heuristic and is dependent on specific tasks. The resulting feature description is usually over-complete, which might mix both important and irrelevant features. Since selected filters are usually non-orthogonal, the information extracted from filter responses are correlated and has to be separated for a precise texture description.

A few researchers have disputed the role and the effectiveness that filter banks are involved in texture analysis. For example, Varma and Zisserman demonstrate an MRF based classifier that uses small neighbourhoods to achieve superior classification results to classifiers based on filter banks [101]. In another work, Gimel'farb et al. point out that large-scale filter-banks bring a too big number of the sufficient signal statistics into the model and result in difficult model identification particularly [35].

Figure 5.1: Filter responses of texture D3, produced by a bank of Gabor filters (3 scales and 4 orientations).

Generic Approach

A generic approach creates a geometric or a probability model for texture description. Two main generic approaches are syntactic and probability models.

Syntactic Models

analyse the geometric structure of textures via spatial analytical techniques. Fractal analysis and structural approach are two main methods used to create syntactic models for textures.

Fractals measure geometric complexity, which could be used to describe many spatial patterns of textures [72]. Conceptually, the word `fractal' refers to complex patterns that recur at various scales but are independent of scales. Since most textures involve patterns with certain degree of self-similarity at different scales, fractal metrics could provide measures of these patterns for texture description. Based on the idea, various fractal models have been proposed for modelling textures in natural scenes [81] and in medical imaging [15].

Structural approaches attempt to derive geometrical representations based on the concept that texture might be viewed as a spatial organisation of texture elements. The structure and the spatial organisation of texture elements are the key components of the resulting models. Texture elements are salient local constructs, representing local spatial organisations of spatially varying image signals. Examples of texture elements include image edges, shapes, and Voronoi polygons [97]. The spatial organisation of texture elements, e.g., periodic structure, is modelled by a set of placement rules, which corresponds to global properties of textures. In an early structural approach [68], for instance, texture elements refer to small elementary regions (windowed sub-pattern) and their placement rules are expressed using a set of tree grammars.

Structural approaches employ a variety of spatial analytical techniques for detecting the periodicity and analysing the regularity of textures in order to recover the geometric structure and placement rules of texture elements. For example, Matsuyama et al. [76] detect texture periodicity by finding the peaks from the Fourier spectrum of a textured image. Similarly, Liu et al. [67] detect the peaks but from the output of autocorrelation functions of a texture. Co-occurrence matrices are also used for recovering the periodicity structure from a texture [80]. Besides various geometric techniques, texture elements can also be retrieved based on statistical measures [79].

Probability Models

generalise the feature based descriptive approach by deriving a probability model from the joint distribution o f selected image features.

A probability model assumes each texture is generated by a particular underlying stochastic process and describe the texture by a model of the generative process. Typically, a probability model is specified by a joint probability distribution of texture features, in which textures are characterised by model parameters.

Generally, it involves two steps to derive a probability model, namely, model creation and identification. Model creation entails selecting texture features into the model and formulating parametric model functions. Model identification is to estimate unknown model parameters for a particular texture. The process is also known as model fitting. Identification of a probability model is solved using statistical inference techniques, e.g., maximum-likelihood estimation (MLE) or Bayesian estimation [27]. MLE assumes that model parameters are unknown but fixed quantitative values. The best estimates of parameters are the values that maximise the probability of obtaining the observed samples. Usually, the log-likelihood function is maximised because it is monotonically increasing. Bayesian estimation assumes model parameters are random variables having known prior distribution. Bayesian estimation yields a weighted average of possible models, still containing uncertainty. MLE could be considered as a special case with uninformative priors of Bayesian estimation. These two methods yield similar results of parameter estimation especially for distributions in exponential families [5].

Markov-Gibbs random fields [6,45,20,13,7,37,113] are the most successful probability models for texture analysis. A thorough discussion about MGRFs will be deferred to the next section. Another recent development of probability models is the combination of the filtering theory with texture modelling. Several probability models are derived from the joint statistics of texture features extracted from the spectral domain. For example, Zhu et al. [113] derived an MGRF model by matching the marginal distributions of filter responses to the empirical ones found in a training image. Portilla and Simoncelli [83,84] proposed a parametric probability model based on joint statistics of complex wavelet coefficients.