|
|
|
|

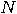 is given and known to be composite, find a
non-trivial factor of it, that is,
is given and known to be composite, find a
non-trivial factor of it, that is, 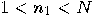 such that
such that 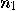 divides
divides 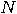 (
(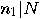 ).
). 


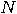 bits; this is exponential with the input size
as
bits; this is exponential with the input size
as 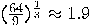 . See Lenstra and Lenstra
_[87], Gruska
_[67]. There
exist sub-exponential O(
. See Lenstra and Lenstra
_[87], Gruska
_[67]. There
exist sub-exponential O(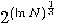 ) randomized algorithms
for factoring.
) randomized algorithms
for factoring.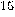

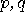 (typically of 512
or 1024 digits). Encription seems to be secure provided it is not feasible
to get
(typically of 512
or 1024 digits). Encription seems to be secure provided it is not feasible
to get 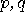 from their product
from their product
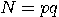 .
.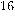 The RSA
method is one of the most popular public key systems and is implemented in
many communication programs.
The RSA
method is one of the most popular public key systems and is implemented in
many communication programs. 



| Year/Number of bits | 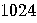 |
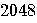 |
4096 |
| _ |  |
 |
 |
| 2006 | 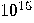 years years
|
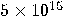 years years
|
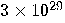 years years
|
 |
 |
 |
|
| 2024 | 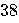 years years
|
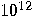 years years
|
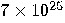 years years
|
 |
 |
 |
|
| 2042 | 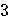 days days
|
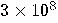 years years
|
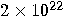 years years
|


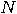 and let us find an integer
and let us find an integer 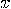 such that
such that 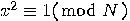 ,
and
,
and 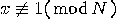 ,
, 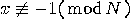 . If
. If 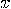 is an integer satisfying the above conditions, then
is an integer satisfying the above conditions, then 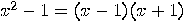 is a multiple of
is a multiple of 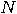 , but
, but 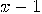 is
not divisible by
is
not divisible by 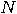 nor is
nor is 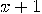 , so there exists a non-trivial factor
, so there exists a non-trivial factor 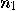 of
of 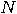 that divides say
that divides say 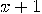 or
or 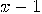 . A factor of
. A factor of 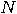 can then be found by Euclid’s algorithm
can then be found by Euclid’s algorithm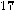 in O(
in O(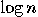 ) time: we compute
) time: we compute 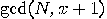 and
and 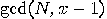 .
. 
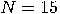 , then
, then 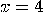 is a solution of
is a solution of 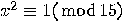 that verifies the above requirements;
that verifies the above requirements; 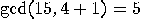 ,
, 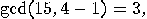 so 5 and 3 are non-trivial divisors of 15.
so 5 and 3 are non-trivial divisors of 15. 
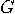 be the set of all integers
be the set of all integers 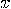 in the interval
in the interval 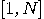 co-primes with
co-primes with 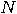 , that is
, that is 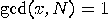 .
.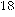 Pick
Pick
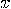 in
in 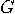 and define the function
and define the function 
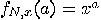 (
(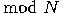 ).
).
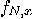 is periodic,
that is there exists an integer
is periodic,
that is there exists an integer  such that
such that
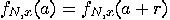 , for every
, for every 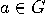 . The smallest
. The smallest  such that
such that 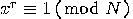 is called the order of
is called the order of 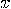 and is denoted
by
and is denoted
by 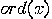 .
. 
 is even, then the equation
is even, then the equation

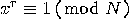

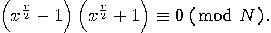
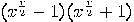 is a multiple
of
is a multiple
of 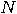 , hence, unless
, hence, unless 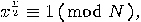 or
or 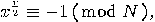 both factors of the product must have a non-trivial factor in common with
both factors of the product must have a non-trivial factor in common with 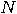 . Consequently, the following algorithm can be used:
. Consequently, the following algorithm can be used: 
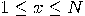 .
.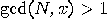 , then we have
a factor of
, then we have
a factor of 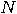 and stop.
and stop. of the function
of the function
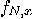 .
. is odd or
is odd or 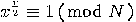 or
or 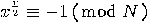 ,
,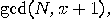
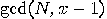 to get a factor of
to get a factor of 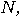 and stop. _
and stop. _
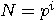 , where
, where 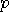 is a prime and
is a prime and 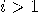 , if
, if 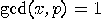 and
and 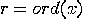 , then
, then
 is odd or
is odd or 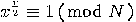 or
or 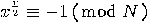 . So, this case is excluded by the above algorithm. However,
we don’t lose generality because power of primes can be factorized by conventional
computers in polynomial time.
. So, this case is excluded by the above algorithm. However,
we don’t lose generality because power of primes can be factorized by conventional
computers in polynomial time. 
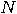 by computing
by computing 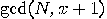 and
and 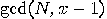 ? This
question is answered by the following evaluations (see, for example, Shor
_[122] or Gruska
[67]):
? This
question is answered by the following evaluations (see, for example, Shor
_[122] or Gruska
[67]): 

If there is a polynomial time deterministic/probabilistic/quantum
algorithm to compute the period of the function 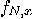 , for every , for every 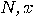 , then there exists a deterministic/probabilistic/quantum
algorithm to factorize any integer , then there exists a deterministic/probabilistic/quantum
algorithm to factorize any integer 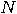 . .  |

 ! Next we will follow Shor
_[122] in presenting
a polynomial time quantum algorithm to compute the period of the function
! Next we will follow Shor
_[122] in presenting
a polynomial time quantum algorithm to compute the period of the function
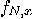 .
. 
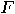 be quantum function
be quantum function 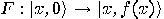 of the integer function
of the integer function 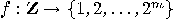 with the unknown period
with the unknown period 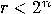 . To determine
. To determine  , we need two registers, with the sizes of
, we need two registers, with the sizes of 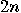 and
and 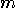 qubits,
which should be reset to
qubits,
which should be reset to 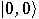 .
. 
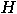 , a homogenous superposition of all basis vectors
in the first register by applying an operator
, a homogenous superposition of all basis vectors
in the first register by applying an operator 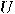 :
: 
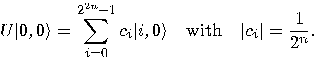
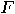 to the resulting state gives:
to the resulting state gives:

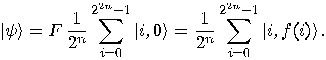
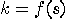 with
with 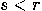 reduces the state to
reduces the state to 
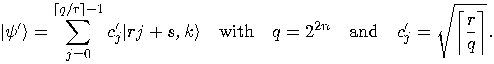
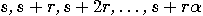 , where
, where 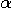 is the largest integer
such that
is the largest integer
such that 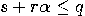 , and
, and 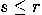 is chosen randomly (by measurement).
So,
is chosen randomly (by measurement).
So, 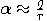 . The post-measurement
state
. The post-measurement
state 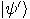 of the first register
consists only of basis vectors of the form
of the first register
consists only of basis vectors of the form 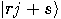 . Reason:
. Reason: 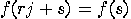 , for all
, for all 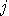 .
. 
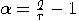 then
then 
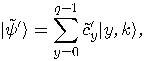

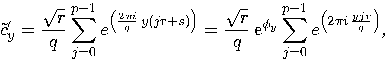

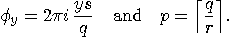

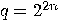 is a multiple of
is a multiple of  , then
, then 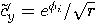 if
if 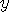 is a multiple of
is a multiple of 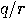 , and
, and 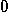 otherwise. But even
if
otherwise. But even
if  is not a power of
is not a power of 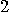 , the spectrum of
, the spectrum of 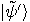 shows distinct peaks with a period of
shows distinct peaks with a period of 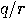 because
because 
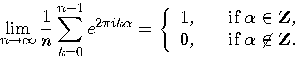
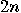 qubits when
qubits when 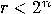 : it guarantees
at least
: it guarantees
at least 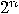 elements in the above sum and
thus a peak width of order O
elements in the above sum and
thus a peak width of order O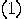 .
. 
 close to
close to 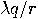 with
with 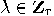 . This can be written as
. This can be written as 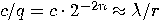 . We can think of this result as a rational approximation
. We can think of this result as a rational approximation
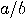 with
with 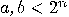 for dyadic number
for dyadic number 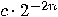 . An efficient classical algorithm for solving
this problem using continued fractions is described in Hardy and Wright [
68] and is implemented in the denominator function.
. An efficient classical algorithm for solving
this problem using continued fractions is described in Hardy and Wright [
68] and is implemented in the denominator function. 
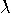 and
and  are
only determined by
are
only determined by 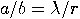 if
if 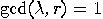 . The probability that
. The probability that 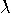 and
and  are
co-prime is greater then
are
co-prime is greater then 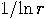 , so only O
, so only O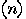 trials are necessary to achieve a probability of success as close to one
as desired; in fact, as observed by Shor _[122], the expected number of trials can be
decreased to a constant.
trials are necessary to achieve a probability of success as close to one
as desired; in fact, as observed by Shor _[122], the expected number of trials can be
decreased to a constant.



Number of bits |
|
|
4,096 |
| Number of qubits
|
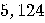 years |
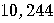 years |
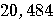 years |
| Number of gates |
 years |
 years years |
 years |
| Factoring time |
 mins |
36 min |
 hours |

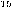 Cf. Vazirani
_[139].
Cf. Vazirani
_[139].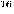 It is not known whether
breaking RSA is as hard as factoring.
It is not known whether
breaking RSA is as hard as factoring. The greatest common divisor
The greatest common divisor 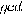 of
of 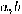 can be computed by the scheme:
can be computed by the scheme: 
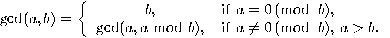 |
 |
 |
 |
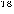 This set is
a group under the multiplication (
This set is
a group under the multiplication ( ).
). Recall that
Recall that 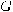 is the set of all integers in the interval
is the set of all integers in the interval
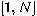 co-primes with
co-primes with 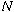 .
. If the supposed period
If the supposed period 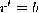 derived form the rational approximation
derived form the rational approximation 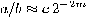 is odd or
is odd or 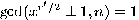 , then one could try to expand
, then one could try to expand
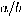 by some integer factor
by some integer factor
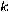 in order to guess the actual period
in order to guess the actual period 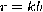 .
.