|
|
|
|

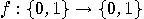 and suppose that we have a black box to compute
it. We would like to know whether
and suppose that we have a black box to compute
it. We would like to know whether  is constant (that is,
is constant (that is, 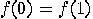 ) or balanced (
) or balanced (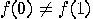 ). To make this test classically, we need two computations of
). To make this test classically, we need two computations of
 ,
, 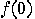 and
and 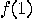 and one comparison. Is it possible to do it better?
The answer is affirmative, and here is a possible solution.
and one comparison. Is it possible to do it better?
The answer is affirmative, and here is a possible solution. 
 . Consider the transformation
. Consider the transformation
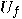 which applies to two qubits,
which applies to two qubits,
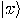 and
and 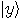 and produces
and produces 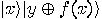 .
.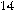 This transformation flips the second qubit
if
This transformation flips the second qubit
if  acting on the first
qubit is 1, and does nothing if
acting on the first
qubit is 1, and does nothing if  acting on the first qubit is 0.
acting on the first qubit is 0. 
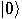 and
and 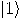 . Assume first that the second
qubit is initially prepared in the state
. Assume first that the second
qubit is initially prepared in the state 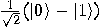 . Then,
. Then, 


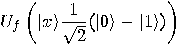  |
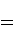  |
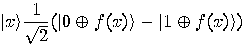  |
  |
  |
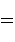  |
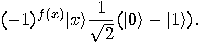  |
  |
  |
  |
  |
  |

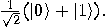 The black box will produce
The black box will produce 

  |
  |
  |
  |
  |
  |
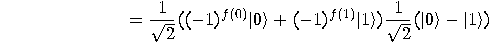  |
  |
  |
  |
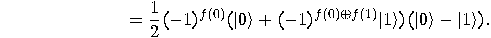  |
  |

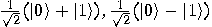 : we will obtain
: we will obtain 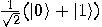 if the function
if the function  is balanced and
is balanced and 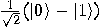 in the opposite case. So, Deutsch’s
problem was solved with only one computation of
in the opposite case. So, Deutsch’s
problem was solved with only one computation of  . The explanation consists in the ability of a
quantum computer to be in a blend of states: we can compute
. The explanation consists in the ability of a
quantum computer to be in a blend of states: we can compute 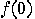 and
and 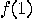 , but also, and more importantly, we can extract
some information about
, but also, and more importantly, we can extract
some information about  which tells us whether
which tells us whether 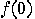 is equal or not to
is equal or not to 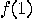 .
. 
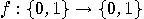 be implemented
by a quantum gate array
be implemented
by a quantum gate array 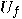 ?
The answer is affirmative. Identifying the values 0 and 1 with the kets
?
The answer is affirmative. Identifying the values 0 and 1 with the kets 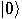 respectively
respectively 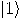 ,
, 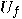 may be defined as the linear operator
may be defined as the linear operator 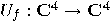 , which satisfies, for any
, which satisfies, for any  the equality
the equality 
 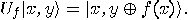 |
(13) |
 we apply
we apply  to
to  . Graphically, the transformation
. Graphically, the transformation 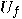 is presented in Figure 14. We shall argue that
is presented in Figure 14. We shall argue that 
for any function 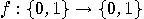 , , 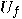 is a unitary transformation. is a unitary transformation.  |

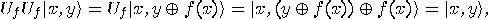
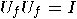 , it suffices to
prove that
, it suffices to
prove that 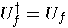 .
. 
 can be defined
in four ways: 1.
can be defined
in four ways: 1. 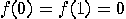 ; 2.
; 2. 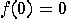 ,
, 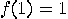 ; 3.
; 3. 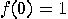 ,
, 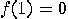 ; and 4.
; and 4. 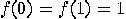 .
. 
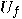 in each situation, taking into account the correspondences:
in each situation, taking into account the correspondences:

 .
.
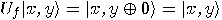 , hence
, hence
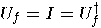 . In the second case,
. In the second case, 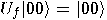 ,
, 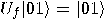 ,
, 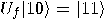 ,
, 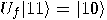 , so it follows
that
, so it follows
that 
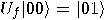 ,
, 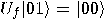 ,
, 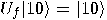 and
and 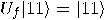 , therefore,
, therefore, 
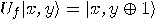 , i.e.
, i.e. 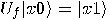 and
and 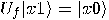 , hence
, hence 

 By
By 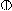 we denote, as
usual, the sum modulo 2.
we denote, as
usual, the sum modulo 2.