|
|
|
|

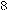 They considered a system of two spatially separated but
quantum mechanically correlated particles. A “mysterious” feature appears:
By counterfactual reasoning, quantum mechanical experiments yield outcomes
which cannot be predicted by quantum theory; hence the quantum mechanical
description of the system is incomplete!
They considered a system of two spatially separated but
quantum mechanically correlated particles. A “mysterious” feature appears:
By counterfactual reasoning, quantum mechanical experiments yield outcomes
which cannot be predicted by quantum theory; hence the quantum mechanical
description of the system is incomplete! 


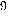 parts, two detectors (D1) and (D2) and a source (S) emitting
particles. The source is placed between the detectors: whenever a button
is pushed on (S), shortly thereafter two particles emerge, moving off toward
detectors (D1) and (D2). Each detector has a switch that can be set in one
of three possible positions – labelled 1,2,3 – and a bulb that can flash
a red (
parts, two detectors (D1) and (D2) and a source (S) emitting
particles. The source is placed between the detectors: whenever a button
is pushed on (S), shortly thereafter two particles emerge, moving off toward
detectors (D1) and (D2). Each detector has a switch that can be set in one
of three possible positions – labelled 1,2,3 – and a bulb that can flash
a red ( ) or a green (
) or a green ( ) light. The purpose of lights is to “communicate"
information to the observer. Each detector flashes either red or green whenever
a particle reaches it. Because of the lack of any relevant connections between
any parts of the device, the link between the emission of particles by (S),
i.e. as a result of pressing a button, and the subsequent flashing of detectors,
can only be provided by the passage of particles from (S) to (D1) and (D2).
Additional tools can be used to check and confirm the lack of any communication,
cf. [97], p. 941.
) light. The purpose of lights is to “communicate"
information to the observer. Each detector flashes either red or green whenever
a particle reaches it. Because of the lack of any relevant connections between
any parts of the device, the link between the emission of particles by (S),
i.e. as a result of pressing a button, and the subsequent flashing of detectors,
can only be provided by the passage of particles from (S) to (D1) and (D2).
Additional tools can be used to check and confirm the lack of any communication,
cf. [97], p. 941.  The device is repeatedly operated as follows:
The device is repeatedly operated as follows: 
| 1. | the switch
of either detector (D1) and (D2) is set randomly to 1 or 2 or 3, i.e. the
settings or states 11, 12, 13, 21, 22, 23, 31, 32, 33 are equally likely,
 |
| 2. | pushing a
button on (S) determines the emission toward both (D1) and (D2),  |
| 3. | sometime later,
(D1) and (D2) flash one of their lights, 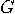 or or 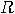 , ,  |
| 4. | every run
is recorded in the form 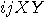 ,
meaning that (D1) was set to state ,
meaning that (D1) was set to state 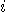 and
flashed and
flashed 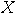 and (D2) was set to and (D2) was set to 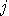 and flashed and flashed 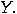  |
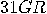 means “(D1) was set to 3 and flashed
means “(D1) was set to 3 and flashed 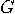 and (D2) was set to 1 and flashed
and (D2) was set to 1 and flashed 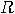 ".
".

| (a) | For records
starting with 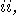 i.e. 11,
22, 33, both (D1) and (D2) flash the same colours, i.e. 11,
22, 33, both (D1) and (D2) flash the same colours, 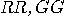 , with equal frequency; , with equal frequency; 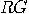 and and 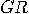 are
never flashed. are
never flashed.  |
| (b) | For records
starting with 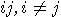 , i.e. 12,
13, 21, 23, 31, 32, both (D1) and (D2) flash the same colour only 1/4 of
the time ( , i.e. 12,
13, 21, 23, 31, 32, both (D1) and (D2) flash the same colour only 1/4 of
the time (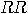 and and 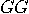 come with equal frequencies); the other 3/4 of the time, they
flash different colours ( come with equal frequencies); the other 3/4 of the time, they
flash different colours (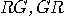 ), occurring again with equal frequencies. ), occurring again with equal frequencies.  |


| H1 | Particles are classified into eight categories:

 |
| H2 | Two particles produced in a given run carry identical
programs.  |
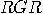 , then both
detectors will flash
, then both
detectors will flash 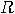 in states 1 and 3;
they will flash
in states 1 and 3;
they will flash 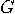 if both are in state 2.
Detectors flash the same colours when being in the same states because particles carry the same programs.
if both are in state 2.
Detectors flash the same colours when being in the same states because particles carry the same programs.
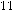



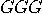 or
or 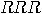 , then
detectors will flash the same colour all the time. For particles carrying
programs containing one colour appearing once and the other colour appearing
twice, only in two cases out of six possible combinations both detectors
will flash the same light. For example, for particles of type
, then
detectors will flash the same colour all the time. For particles carrying
programs containing one colour appearing once and the other colour appearing
twice, only in two cases out of six possible combinations both detectors
will flash the same light. For example, for particles of type 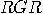 , both detectors will flash
, both detectors will flash 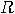 if (D1) is in state 1 and (D2) is in state
3 and vice versa. In all remaining cases detectors will flash different lights.
The argument remains the same for all combinations as the conclusion was
solely based on the fact that one colour appears once and the other twice.
So, the lights are the same one third of the time.
if (D1) is in state 1 and (D2) is in state
3 and vice versa. In all remaining cases detectors will flash different lights.
The argument remains the same for all combinations as the conclusion was
solely based on the fact that one colour appears once and the other twice.
So, the lights are the same one third of the time. 


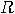 ) or green (
) or green (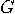 ). Again, detectors are supposed to be far away from the source
and there are no connections between the source and detectors (except those
induced by a group of particles flying from the source to each detector).
). Again, detectors are supposed to be far away from the source
and there are no connections between the source and detectors (except those
induced by a group of particles flying from the source to each detector).


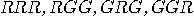 , and
they are equally likely, (b) if all detectors are set to 1, then an odd number
of red lights is never flashed:
, and
they are equally likely, (b) if all detectors are set to 1, then an odd number
of red lights is never flashed: 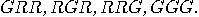

 telling its detector to flash colour
telling its detector to flash colour  if in state 1 and colour
if in state 1 and colour 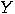 if in state 2. There are four types of programs:
if in state 2. There are four types of programs:
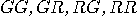 . A run in which programs
carried by the trio of particles are of types (
. A run in which programs
carried by the trio of particles are of types (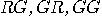 ) will result in
) will result in 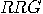 if the states were 122, in
if the states were 122, in 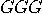 if the states were 212, and in
if the states were 212, and in 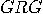 if the states were 221. This is an illegal set
of programs as the number of
if the states were 221. This is an illegal set
of programs as the number of 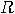 ’s is not
odd (in
’s is not
odd (in 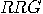 , for example). A legal set
of programs is
, for example). A legal set
of programs is 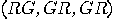 as it produces
as it produces
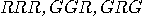 on 122, 212, 221. There
are eight legal programs,
on 122, 212, 221. There
are eight legal programs, 

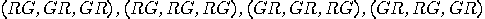

 ’s to be flashed
on 111, but quantum mechanics prohibits this in every 111 run.
’s to be flashed
on 111, but quantum mechanics prohibits this in every 111 run. 
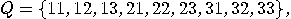 the input alphabet models the
lights, red and green,
the input alphabet models the
lights, red and green, 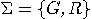 ,
the output alphabet captures all combinations of lights flashed by (D1) and
(D2),
,
the output alphabet captures all combinations of lights flashed by (D1) and
(D2), 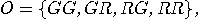 and the output function
and the output function
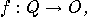 modeling all combinations
of green/red lights flashed by (D1) and (D2) in all their possible states,
is probabilistically defined by:
modeling all combinations
of green/red lights flashed by (D1) and (D2) in all their possible states,
is probabilistically defined by: 


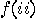  |
  |
  |
  |
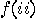  |
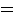  |
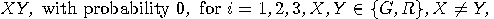  |
  |
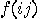  |
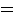  |
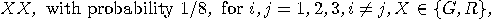  |
  |
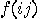  |
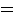  |
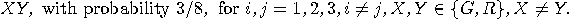  |
  |
  |
  |
  |
  |

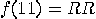 with probability
1/2,
with probability
1/2, 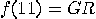 with probability 0,
with probability 0,
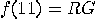 with probability 0,
with probability 0, 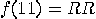 with probability 1/2,
with probability 1/2, 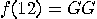 with probability 1/8,
with probability 1/8, 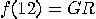 with probability 3/8,
with probability 3/8, 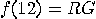 with probability 3/8,
with probability 3/8, 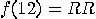 with probability 1/8, etc.
with probability 1/8, etc.

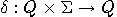 is not specified. In fact, varying all transition functions
is not specified. In fact, varying all transition functions 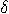 we get a class of Mermin EPR automata:
we get a class of Mermin EPR automata: 
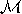 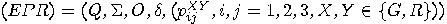 , ,  |

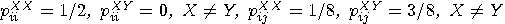 .
. 

    |
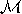
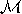
 is isomorphic
to a Mermin’s automaton
is isomorphic
to a Mermin’s automaton 
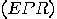 , i.e.,
, i.e., 
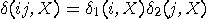 , and
, and 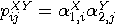 , for all
, for all 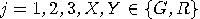 ?
? 

no single state of any Mermin’s EPR probabilistic
automaton 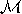 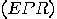 can be simulated by the product of the corresponding
states of any probabilistic automata can be simulated by the product of the corresponding
states of any probabilistic automata 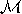 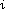 . .  |
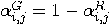 . For a state
. For a state 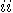 we get the following contradictory relations:
we get the following contradictory relations: 
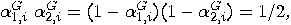
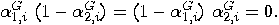
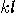 with
with 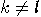 we, again, get two contradictory relations:
we, again, get two contradictory relations: 
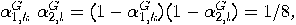
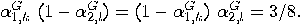
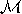
 has strong correlations preventing
it from being decomposed as a direct product of two independent probabilistic
automata, no matter what transitions and output functions.
has strong correlations preventing
it from being decomposed as a direct product of two independent probabilistic
automata, no matter what transitions and output functions. 

 If, without in any way disturbing a system, we
can predict with certainty (i.e. with probability equal to unity) the value
of a physical quantity, then there exists an element of physical reality
corresponding to this physica quantity. See [55], p. 777.
If, without in any way disturbing a system, we
can predict with certainty (i.e. with probability equal to unity) the value
of a physical quantity, then there exists an element of physical reality
corresponding to this physica quantity. See [55], p. 777. There are no relevant
connections, neither mechanical nor electromagnetic.
There are no relevant
connections, neither mechanical nor electromagnetic. The emitting source (S) has no knowledge about the
states of (D1) and (D2) and there is no communication among any parts of
the device.
The emitting source (S) has no knowledge about the
states of (D1) and (D2) and there is no communication among any parts of
the device.