|
|
|
|

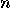 -bit register
of memory can exist in any of
-bit register
of memory can exist in any of 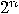 logical
states, from
logical
states, from  (
(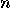 zeros) to
zeros) to  (
(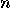 ones).
ones). 
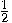 particle, when measured, is
always found to be in one of two possible states, represented as
particle, when measured, is
always found to be in one of two possible states, represented as 

 -qubit system can exist in any superposition
of the form
-qubit system can exist in any superposition
of the form 
 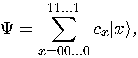 |
(5) |
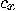 are (complex) numbers such that
are (complex) numbers such that 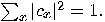 The exponential “explosion"
represented by formula (5) distinguishes
quantum systems from classical ones: in a classical system, which is completely
described locally, a state is described by a number of parameters growing
only linearly with the size of the system, but, as we shall see in the next
section, quantum systems may not admit such a description (because quantum
states may be “entangled").
The exponential “explosion"
represented by formula (5) distinguishes
quantum systems from classical ones: in a classical system, which is completely
described locally, a state is described by a number of parameters growing
only linearly with the size of the system, but, as we shall see in the next
section, quantum systems may not admit such a description (because quantum
states may be “entangled"). 
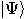 invented by Paul Dirac [54]. Row vectors, such as
invented by Paul Dirac [54]. Row vectors, such as 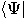 , are known as “bra" vectors;
when you put together a column and a bra vector, you get a bracket, that
is the inner product of the two vectors,
, are known as “bra" vectors;
when you put together a column and a bra vector, you get a bracket, that
is the inner product of the two vectors, 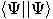 , also written as
, also written as 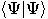 .
. 

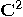 , a two dimensional space. Assume that a particular
complete orthonormal basis, denoted by
, a two dimensional space. Assume that a particular
complete orthonormal basis, denoted by 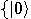 ,
, 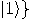 , has been fixed. These vectors,
, has been fixed. These vectors, 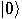 and
and 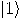 , correspond to the classical bit values 0 and 1, respectively.
, correspond to the classical bit values 0 and 1, respectively.

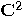 ,
so for each qubit
,
so for each qubit 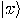 , there
are two (complex) numbers
, there
are two (complex) numbers 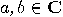 such that
such that 
 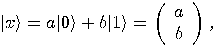 |
(6) |

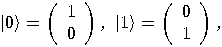
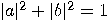 .
. 
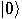 and
and 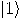 . The angle through which the
vector is rotated about the vertical axis induces the so-called “phase".
So, different qubits may have the same proportion of
. The angle through which the
vector is rotated about the vertical axis induces the so-called “phase".
So, different qubits may have the same proportion of 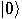 and
and 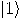 , but with different phase factors. Phase is irrelevant
for the whole states but it’s crucial for “quantum interference effects".
, but with different phase factors. Phase is irrelevant
for the whole states but it’s crucial for “quantum interference effects".

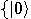 ,
, 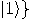 . Then we will obtain the outcome
. Then we will obtain the outcome 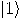 with probability
with probability  , and the outcome
, and the outcome 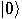 with probability
with probability 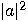 . With the exception of limit
cases
. With the exception of limit
cases 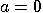 and
and 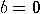 , the measurement irrevocably
disturbs the state: If the value of
the qubit is initially unknown, then there is no way to determine
, the measurement irrevocably
disturbs the state: If the value of
the qubit is initially unknown, then there is no way to determine  and
and 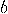 with
any conceivable measurement. However, after
performing the measurement, the qubit
has been prepared in a known state (either
with
any conceivable measurement. However, after
performing the measurement, the qubit
has been prepared in a known state (either 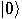 or
or 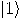 ); this state is typically different from the previous state.
); this state is typically different from the previous state.



 and
and
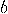 in (6
) encode more than just the probabilities of the outcomes of a measurement
in the
in (6
) encode more than just the probabilities of the outcomes of a measurement
in the 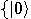 ,
, 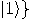 basis. For example, the relative
phase of
basis. For example, the relative
phase of  and
and 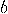 is crucial.
is crucial. 
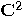 , i.e.
the space
, i.e.
the space 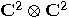 . Using Dirac notation, if
. Using Dirac notation, if 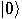 and
and 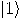 are the vectors of a basis in
are the vectors of a basis in 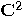 then, the set
then, the set 
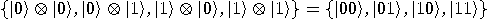
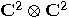 ; more precisely,
; more precisely, 
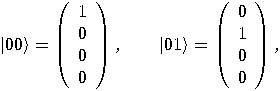

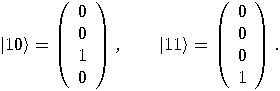
 qubits is represented by
qubits is represented by  copies of
copies of  tensored together. Therefore, the state space is
tensored together. Therefore, the state space is 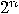 dimensional. A natural basis for this space
consists of
dimensional. A natural basis for this space
consists of 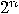 tensor products:
tensor products: 
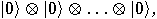
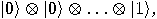

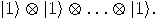
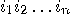 with
with 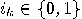 ,
, 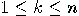 , corresponds to the quantum
state
, corresponds to the quantum
state 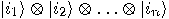 which is simply denoted
by
which is simply denoted
by 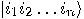 . If
. If 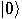 and
and 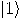 are orthogonal unit vectors in
are orthogonal unit vectors in 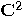 , then the set
, then the set 
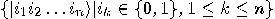
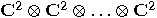 .
. 

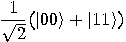

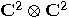 is spanned
by the set
is spanned
by the set 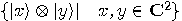 , the existence
of entangled states proves that the previous set is not a linear space. One
can easily find entangled states in an
, the existence
of entangled states proves that the previous set is not a linear space. One
can easily find entangled states in an 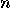 qubit system, for any integer
qubit system, for any integer 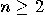 .
. 

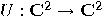 can be viewed as a single qubit gate. Considering
the basis
can be viewed as a single qubit gate. Considering
the basis 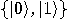 , the transformation
is fully specified by its effect on the basis vectors. In order to obtain
the associated matrix of an operator
, the transformation
is fully specified by its effect on the basis vectors. In order to obtain
the associated matrix of an operator 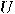 ,
we put the coordinates of
,
we put the coordinates of 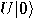 in the first column and the coordinates of
in the first column and the coordinates of 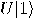 in the second one. So, the
general form of a transformation that acts on a single qubit is a
in the second one. So, the
general form of a transformation that acts on a single qubit is a 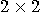 matrix
matrix 
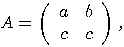
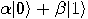 into the
state
into the
state 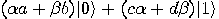 :
: 
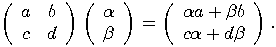
 , the rotation
, the rotation
 is given by
is given by 
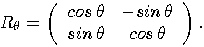
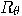 acts as follows:
acts as follows: 
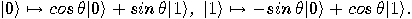
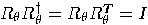 , hence
, hence 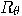 is unitary. Note that in the
special case
is unitary. Note that in the
special case 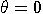 we get the identity transformation
of
we get the identity transformation
of 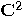 :
: 
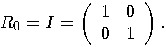
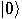 and
and 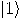 , is given by
, is given by  , that is the matrix
, that is the matrix 
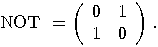

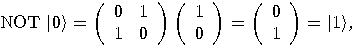

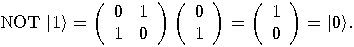
 is defined by the following
operator:
is defined by the following
operator:  so
so 
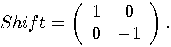
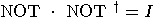 and
and 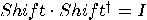 , the operators NOT and
, the operators NOT and 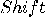 are also unitary. The operator
are also unitary. The operator 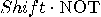 is also a unitary transformation
and we have:
is also a unitary transformation
and we have: 
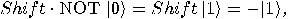
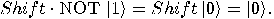

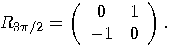

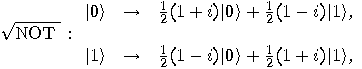

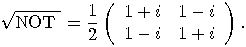

  |
(7) |


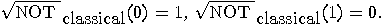

 is defined by
is defined by 
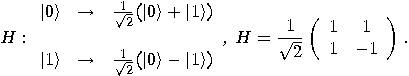
 ,
, 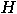 creates a superposition state
creates a superposition state 
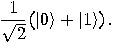
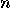 bits individually,
bits individually, 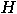 generates a superposition of all
generates a superposition of all 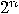 possible states. To see this we need some
rudiments on tensor products.
possible states. To see this we need some
rudiments on tensor products. 
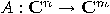 and
and 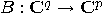 . The tensor product of
. The tensor product of 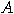 and
and 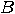 is
the operator
is
the operator 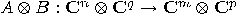 , with the property
, with the property 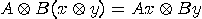 , for any
, for any 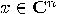 and
and 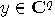 . A convenient way is, again, to work with matrices. Let
. A convenient way is, again, to work with matrices. Let 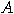 be a
be a 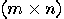 matrix and
matrix and 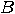 a
a 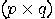 matrix. The (right) Kronecker
product of
matrix. The (right) Kronecker
product of 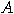 and
and 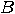 is the
is the 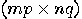 matrix
defined as follows:
matrix
defined as follows: 
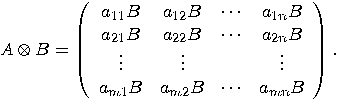

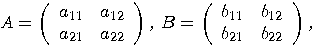
 matrices, then we have:
matrices, then we have: 
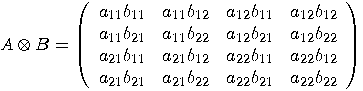

(a) If 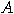 and and 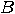 are matrices associated to the operators are matrices associated to the operators 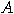 and and 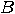 , then
the matrix associated to , then
the matrix associated to 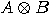 is the Kronecker
product of is the Kronecker
product of 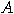 and and 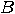 . . (b) The tensor products of two unitary transformations is also unitary. _  |
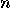 single qubit transformations, we can
obtain examples of unitary transformations acting on
single qubit transformations, we can
obtain examples of unitary transformations acting on 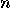 qubits.
qubits. 
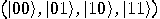 be the
basis in
be the
basis in 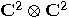 . Then,
. Then, 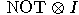 can be expressed as
can be expressed as 
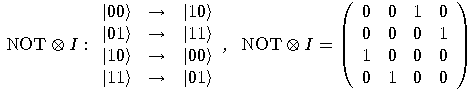

 will be written as
will be written as 
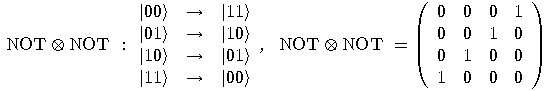 .
. 
 to
to 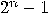 via
Hadamard operator. The Walsh–Hdamard transformation is defined recursively
by
via
Hadamard operator. The Walsh–Hdamard transformation is defined recursively
by 
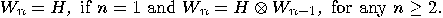
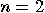 then
then 





























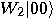  |
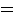  |
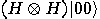  |
  |
  |
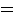  |
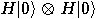  |
  |
  |
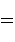  |
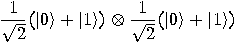  |
  |
  |
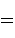  |
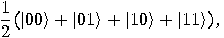  |
  |
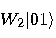  |
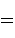  |
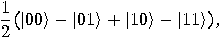  |
  |
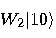  |
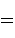  |
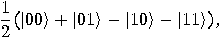  |
  |
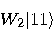  |
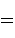  |
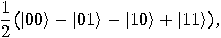  |
  |


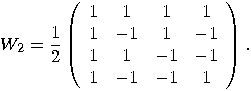

 we get a superposition of all possible states:
we get a superposition of all possible states:













  |
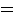  |
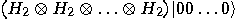  |
  |
  |
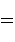  |
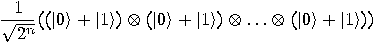  |
  |
  |
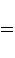  |
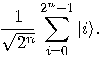  |
  |

 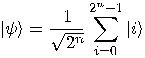 |
(8) |

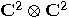 is the “controlled-NOT" gate, _
is the “controlled-NOT" gate, _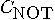 defined as follows:
defined as follows: 
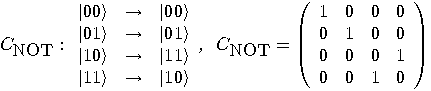 .
. 
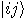 ,
,
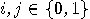 , the output state produced
by
, the output state produced
by 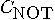 is
is 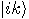 , where
, where 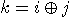 (mod 2). The first bit is not
disturbed (it is a control bit) and the second one interchanges 0 and 1 if
and only if the first bit is 1, which corresponds to the logical exclusive-OR
(XOR). The transformation
(mod 2). The first bit is not
disturbed (it is a control bit) and the second one interchanges 0 and 1 if
and only if the first bit is 1, which corresponds to the logical exclusive-OR
(XOR). The transformation 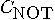 is unitary. Its main feature is given by the following property:
is unitary. Its main feature is given by the following property:

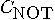 cannot be written as a tensor product of two operators. cannot be written as a tensor product of two operators.  |
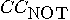 , operating
on three qubits, which negates the rightmost bit if and only if the first
two are both
, operating
on three qubits, which negates the rightmost bit if and only if the first
two are both  :
: 
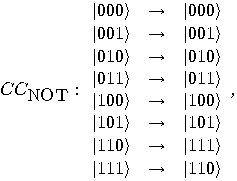

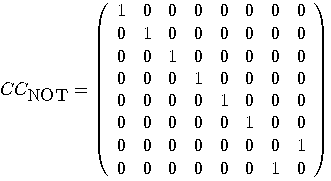 .
. 

