

Next: FRAME model
Up: Auto-models
Previous: Auto-binomial Model
[13,18] assume that the
conditional probability
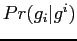 of a pixel is a normal
distribution over an
of a pixel is a normal
distribution over an
 neighbourhood, which is specified
as follows,
neighbourhood, which is specified
as follows,
![$\displaystyle Pr({g}_i \mid {g}^i)=\frac{1}{\sqrt{2\pi{\sigma}^2}}\exp\{-\frac{1}{2{\sigma}^2}[{g}_i-\mu({g}_i \mid {g}^i)]^2\}$](img152.png) |
(5.2.19) |
Here,
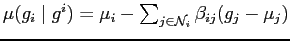 is the conditional mean
and
is the conditional mean
and 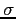 is the conditional variance (standard deviation).
is the conditional variance (standard deviation).
By Markov-Gibbs equivalence, an auto-normal model is specified by
the following joint probability density:
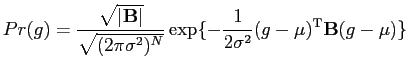 |
(5.2.20) |
where
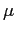 is an
is an
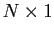 vector of the conditional
means, and
vector of the conditional
means, and
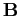 is an
is an
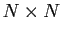 interaction matrix with
unit diagonal elements, the off diagonal element at the position
interaction matrix with
unit diagonal elements, the off diagonal element at the position
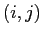 being
being
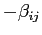 . Since the model distribution in
Eq. (5.2.20) is Gibbsian and also Gaussian, an
auto-normal model is also known as a Gaussian-Markov random
field model.
. Since the model distribution in
Eq. (5.2.20) is Gibbsian and also Gaussian, an
auto-normal model is also known as a Gaussian-Markov random
field model.
An auto-normal model defines a continuous Gaussian MRF. The model
parameters,
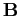 ,
,
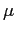 , and
, and 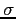 , can be
estimated using either MLE or pseudo-MLE methods [7]. In
addition, a technique representing the model in the spatial
frequency domain [13] has also been proposed for
parameter estimation.
, can be
estimated using either MLE or pseudo-MLE methods [7]. In
addition, a technique representing the model in the spatial
frequency domain [13] has also been proposed for
parameter estimation.


Next: FRAME model
Up: Auto-models
Previous: Auto-binomial Model
dzho002
2006-02-22
![$\displaystyle Pr({g}_i \mid {g}^i)=\frac{1}{\sqrt{2\pi{\sigma}^2}}\exp\{-\frac{1}{2{\sigma}^2}[{g}_i-\mu({g}_i \mid {g}^i)]^2\}$](img152.png)
![$\displaystyle Pr({g}_i \mid {g}^i)=\frac{1}{\sqrt{2\pi{\sigma}^2}}\exp\{-\frac{1}{2{\sigma}^2}[{g}_i-\mu({g}_i \mid {g}^i)]^2\}$](img152.png)
![]() is the conditional mean
and
is the conditional mean
and ![]() is the conditional variance (standard deviation).
is the conditional variance (standard deviation).
![]() ,
,
![]() , and
, and ![]() , can be
estimated using either MLE or pseudo-MLE methods [7]. In
addition, a technique representing the model in the spatial
frequency domain [13] has also been proposed for
parameter estimation.
, can be
estimated using either MLE or pseudo-MLE methods [7]. In
addition, a technique representing the model in the spatial
frequency domain [13] has also been proposed for
parameter estimation.