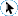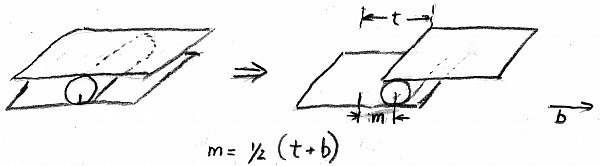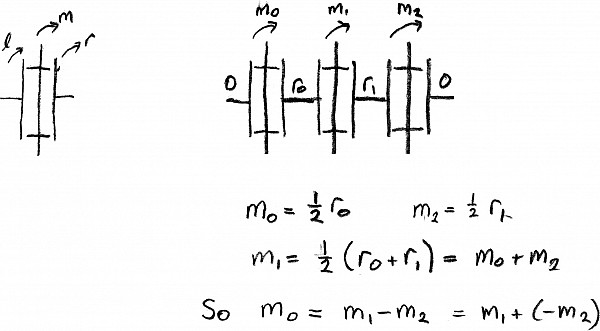First Automatic Totalisator: How Shaft Adders Work

Sorry to insult the technically savvy but let's get down to basics. Consider a roller (could be a pencil) between two sheets of cardboard:

If you keep the lower sheet fixed and move the top sheet without slipping you will find that the roller moves half the distance that the top sheet moves. The same happens if you move the bottom sheet and keep the top fixed so we come up with the fact that the roller moves a distance 1/2 the sum of the two sheet movements - the roller, in fact, adds distances.

Getting more sophisticated, now replace the sheets of cardboard with disks that rotate around a shaft and replace the roller by a pair of wheels that may freely rotate on a housing that itself can rotate around the central shaft - on the left of the diagram below. These wheels are said to be "epicyclic" or "planetary".

Now close up the gap between the disks so that the wheels may rotate without slipping (in practice there will be gears to ensure that there is no slipping.) You can see that the situation is just like that with the roller, the distance moved by each wheel, at the wheel, is 1/2 the sum of the distances moved by the disks at the wheel. Because the distance moved is proportional to the angle moved times the radius (and the same radius applies to the disks and the wheel mounting) we can conclude that the angle moved by the wheel housing is 1/2 the sum of the angles moved by the disks.

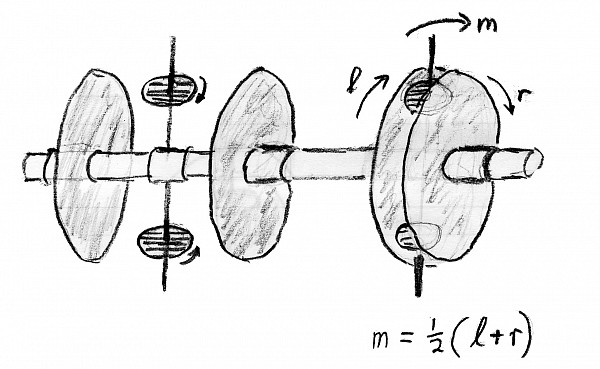
Now let's make things easy by using a bit of algebra. You can abstract the disk/wheel mechanism to the diagram on the left. Now put three of the disk/wheel devices on the same shaft but weld adjacent disks together so that they must move through the same angle. Also, fix the outer wheels so that they do not move.

Write down the equations for the movement of the three disk/wheels and you find that the movement of the leftmost wheel housing is the movement of the middle housing less the movement of the right housing. So, if the left is regarded as output then it will move an angle which is the sum of the angles moved by the middle and the right, if the latter's rotation is regarded as being in the other direction. (If you keep the middle housing fixed what happens is that its wheels transfer the movement from the right to the left but change the direction of movement.) You can tie as many disk/wheel units to the shaft as you like and will find that the leftmost is the sum (with signs) of the other rotations. And you can extend further to the left and have the middle represent the sum of rotations on both sides.

All that is required to complete our shaft adder is to place each planetary wheel housing inside its own wheel, somehow, so that each housing may be rotated by its wheel.

Note that the outer wheels on the left and right do not have to be fixed. They may also be attached to escapements, in which case they need to rotate by twice the distance to impart the same rotation to the central shaft as for the other wheels. Later adders made use of this detail to register bets on the extremities at half the value of those registered by other wheels.