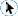Computing History Displays: Fifth Floor - Logic, Switching and Circuits

Technology and mathematics often progress hand-in-hand. When a scientist or engineer needs to describe a new development it is often found that the mathematics needed is already available, often only recently developed. Even before the first stored-program computer was set operating Alan Turing had developed the theory of computing in his exploration of the foundations of mathematics. Here we will see how mathematical logic was adapted to assist with design of telephone switches and exchanges, how some early computers were built using telephone technology, and how mathematical logic has become an essential tool for the design of computer circuits.

The English mathematician George Boole, working from Queens University of Cork in Ireland, in his “Laws of Thought,” of 1854 showed how algebra could be adapted to describe logic instead of arithmetic. Variables, which in Mathematics identify numbers, are restricted to referring to two values only, true and false. The mathematical operators addition and multiplication become disjunction (or) and conjunction (and) of logic. A few more rules or axioms are needed to make it all work but basically the old algebra is adapted with very little change so that it makes statements about logic rather than arithmetic. This new version of algebra became known as Boolean algebra and its inventor is remembered in the “boolean” variables of programming languages such as Java.

Precise logical argument remained the domain of logicians and philosophers, such as Lewis Carroll (the Rev. Charles Dodgson) for many years. Carroll invented many whimsical logical arguments for students to practise their skill. Here is a typical example:

There are many different notations used for Boolean algebra, but with the symbols commonly used in computer design we could describe the argument above as (-D + -W).(-O + W).(-P + D) and show, by manipulating the formula, that it is equivalent to the conclusion (-P + -O). To see some more of Carrol's whimsy, and a better notation for this kind of argument, visit, for example, this delightful page from the University of Hawaii.

Nowadays logical argument is used most often by programmers when they reason about their programs informally, in particular when correcting programs that do not work as expected. Boolean algebra, however, remains central to computer circuit design, as we shall see.

Later, and at the other extreme of practicality, the 19th century saw the invention of the telephone. As use of telephones grew exponentially, telephone companies, whether state or privately owned, grew to become among the largest businesses in the world and this first real IT industry became the largest business sector in many countries. The growth in telephony in first half of the 20th century led to the development of automatic exchanges to connect the originator of a telephone call to a desired destination. This involved the invention of many clever and ingeneous electromechanical devices. On display are some examples, from early-mid 20th century, retained from the Wellesley Street exchange before it was demolished (the exchange building is now part of the Auckland Art Gallery.)

Establishing a telphone call required that a physical link be made in the exchanges between the wires leaving the dialer's telephone and the wires going to the destination. Exchanges shared common wire paths to establish the link. Each user connected to an automatic exchange had dedicated hardware - in some exchanges such as this example the user’s unique hardware included a “uniselector” as packaged in this device. When a user lifted the handset the associated uniselector (the circular switch) would commence to rotate to find a path in the exchange not being used for another call and when found would signal the caller to “go ahead” with a “dial tone”.

Crossbar switch

Later exchanges used “crossbar switches” to help make connections. By swiveling a vertical bar to the right or left, and then swiveling a horizontal bar, a connection was made between a vertical input line and a horizontal output line. Once connected, the horizontal bar was fixed and the contact maintained while the vertical bar, and other horizontal bars, could make further connections. This two-dimensional connection idea is still used in modern switches and memory chips.

Dialed Number Register

Telephone circuits made much use of a simple electomagnetic switches called “relays” Relays are quite clever devices that we will consider further below. By connecting them in different ways it was possible to make simple decisions and remember data. This block of relays was used to remember or register a telephone number as it was dialed, each digit of the number being transmitted as a sequence of pulses. This device was likely built in Antwerp Belgium in the 1920s by the international arm of Western Electric.

A relay is an electromagnetic that is used to control a switch. When electric current is allowed to flow in the electromagnet it pulls a lever that closes the point contacts of the switch. In this photo of an early 20th century relay you can see the cylindrical magnet in the background and the switch point contacts at the top. Because the magnet is bigger and more expensive than the switches, the one relay was often used to operate more than one switch. In fact, as well as closing some switches, turning a circuit on, the one relay could also open another switch and turn another circuit off. Some relays would open then close a switch and others could be used to control the power to operate the relay itself. In summary each relay was a complicated device; however, ad-hoc techniques for connecting relay switches were gradually developed to allow complex devices like the above register to be designed.

Over time, relays were made smaller and faster. Exchanges were given more function and it became clear that relays could be adapted to perform quite general calculations and operate much more quickly than mechanical calculators. Around the mid-century this led to the development of large programmed calculators that used relays to perform the arithmetic while the programs were punched on cards, often a continuous band of cards. These machines were developed in the 1940s and briefly reigned over the world of computation. The most significant being those of Konrad Zuse in Germany, by Stibitz at Bell Telephone Labs and Aiken and IBM at Harvard in the USA. In 1948, a large such calculator of the same style, although partly electronic, the SSEC (Selective Sequence Electronic Calculator) was installed by IBM in New York on prominent public view, see the photo below.

When the first computers were being built in the 1950s the circuits from which they were constructed were for a long time referred to as “switching circuits.” despite the fact that they had replaced relays with electronic switches.

The Harvard Mark I computer was a programmed calculator constructed from relays, very similar to those used in telephone exchanges. These machines were used to compute tables of trigonometric and other mathematical functions, in particular Bessel functions, hence the nickname of Bessie for the machine.

Computer folk lore tells us that the first ever “bug” in a computer was found by Grace Hopper, an operator of the Mark 1 computer, caught within one of the it’s relays. We have a wooden sculpture by the artist, Leigh Christensen that celebrates the story of Bessie and the first computer bug as told by Grace Hopper in her letter to journal Annals of the History of Computing. Look closely at the relays to see the bug's life cycle, but also step back to consider whether the whole machine might be the beginning of a line of threatening “bugs.”

We have more details on the sculpture and on Harvard Mark 1 and the bug. Sadly, it is now thought that the term “bug” was in use long before Bessie was built. It is also not certain whether the bug was found in 1945 or 1947 and whether the calculator was the Mark I or its successor the Mark II.

For illustrations to accompany this section look here.

Charles Pierce, an American Philosopher, recognised in 1895 that the operators of Boolean algebra can be implemented in circuits by using switches. Pierce is also known for the invention of what we call today the nand gate.

However, it was not until 1938 that Claude Shannon (better known as the originator of Information Theory) in his 1938 Master of Science thesis at MIT showed how Boolean algebra could be applied to the design of circuits involving switches. For example, taking "current flowing" to be true and current not flowing to be false, the behaviour of basic computer circuits can be summarized by equations of Boolean algebra. Mathematics can then be used to describe and simplify computer circuits.

When the very first electronic computers were designed their circuits tended to be described by detailed electronic circuit diagrams. It became clear that it was a sound design practice to separate the design of the electronics of switches from the conceptual way that they were connected together. Thus computer circuits came to be called "logic circuits" and described using diagrams with "logic gates" as the basic elements. The logic gates perform the simple operations of Boolean algebra "and" (output true only when all inputs are true), "or" (output true when any input is true and "not" (output the opposite of the input.) In practice the gates are combined together in circuit elements - for example Pierce's "nand", and followed by a not, which by itself allows the construction of any circuit.

Logic gates are constructed from switches, at first using electromechanical relays then, when developed, electronic switches. The first extensive use of logic gate symbols was by Turing in his 1945 design proposal for the ACE computer where he followed a suggestion of von Neumann's and adapted a notation used by McCulloch and Pitts to describe neural networks. The symbols for logic gates were later standardized.

Although Boolean algebra was used in developing the theory of computer circuits, for arithmetic in particular, engineers preferred circuit diagrams for detailed descriptions. Boolean algebra was often used in the early stages of developing a computer, as in the example of design by Dr Gene Amdahl of the Amdahl 580 computer as recently as the late 1970s. Since that time, design automation has meant that the use of Boolean algebra is the normal approach to specifying computer circuits, with the definition of the circuits themselves an automated process performed by software, though often the circuit descriptions more resemble programs in a special language.

It is only recently that technologies have been proposed in which gates are implemented by other than switches. One example, the Billiard Ball model, considers the collision of elastic balls as performing logic operations. But these ideas have yet to be put into practice and up till now all computers have been designed with switches as their basic elements.