Spatial Frequency Domain

Spatial frequency

Images are 2D functions f(x,y) in spatial coordinates (x,y) in an image plane. Each function describes how colours or grey values (intensities, or brightness) vary in space:

Variations of grey values for different x-positions along a line y = const.

An alternative image representation is based on spatial frequencies of grey value or colour variations over the image plane. This dual representation by a spectrum of different frequency components is completely equivalent to the conventional spatial representation: the direct conversion of a 2D spatial function f(x,y) into the 2D spectrum F(u,v) of spatial frequencies and the reverse conversion of the latter into a spatial representation f(x,y) are lossless, i.e. involve no loss of information. Such spectral representation sometimes simplifies image processing.

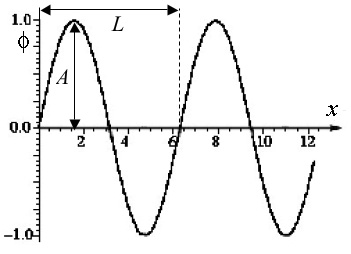
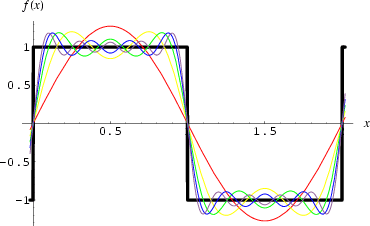
To formally define the term "spatial frequency", let us consider a simple 1D periodic function such as sine function φ(x) = sin x:

Periodic function φ(x) = sin x General sinusoidal function x

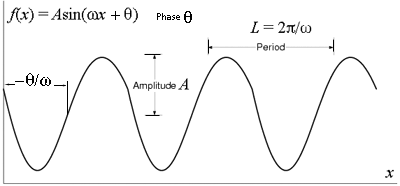
It consists of a fixed pattern or cycle (from x = 0 to x = 2π ≅ 6.28; in particular, φ(0) = 0.0; φ(π/2) = 1.0; φ(π) = 0.0; φ(3π/2) = −1.0; and φ(2π) = 0.0) that repeats endlessly in both directions. The length of this cycle, L (in the above example L = 2π) is called the period, or cycle of the function, and the frequency of variation is the reciprocal of the period. For the spatial variation where L is measured in distance units, the spatial frequency of the variation is 1/L. Generally, a sinusoidal curve f(x) = A sin(ωx + θ) is similar to the above pure sine but may differ in phase θ, period L = 2π/ω (i.e. angular frequency ω), or / and amplitude A. The sine function has the unit amplitude A = 1, the unit spatial frequency (i.e. the angular frequency ω = 2π), and the zero phase θ = 0.

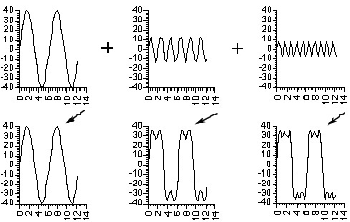
Images below show what x-directed sinusoidal variations of grey values in a synthetic greyscale image f(x,y) = fmean + A sin((2π/N)ux + θ) look like:

Column1: the bottom image is half the amplitude/contrast of the top image.
Column 2: the bottom image is twice the spatial frequency of the top image.
Column 3: the bottom image is 90o (θ = π/2) out of phase w.r.t. the top image.
(All the images - from www.luc.edu/faculty/asutter/sinewv2.gif)

Here, u is a dimensionless spatial frequency corresponding to the number of complete cycles of the sinusoid per the image width N measured in the number of pixels. The ratio 2π/N gives the spatial frequency in units of cycles per pixel. To relate the dimensionless spatial frequency parameter u to the number of complete cycles of the sinusoid that fit into the width of the image from the starting pixel position x = 0 to the ending position x = N − 1, the function should be specified as f(x,y) = fmean + A sin((2π/(N−1))ux + θ) so that u corresponds to the number of complete cycles that fit into the width of the image.

A few examples of more general 2D sinusoidal functions (products of x- and y- oriented sinusoids:

Images from: www.canyonmaterials.com/grate4.html www.xahlee.org/SpecialPlaneCurves_dir/Sinusoid_dir/sinusoid.html

In such artificial images, one can measure spatial frequency by simply counting peaks and thoughs. Most of real images lack any strong periodicity, and Fourier transform is used to obtain and analyse the frequencies.

Return to the local table of contents

Fourier transform

The key idea of Fourier's theory is that any periodic function, however complex it is along the period, can be exactly (i.e. with no information loss) represented as a weighted sum of simple sinusoids. Irrespectively of how irregular may be an image, it can be decomposed into a set of sinusoidal components having each a well-defined frequency. The sine and cosine functions for the decomposition are called the basis functions of the decomposition. The weighted sum of these basis functions is called a Fouirier series

where the weighting factors for each sine (an) and cosine (bn) function are the Fourier coefficients, and the index n specifying the number of cycles of the sinusoid that fit within one period L of the function f(x) is a dimensionless frequency of a basis function. A 1D function with period L is uniquely represented by two infinite sequences of coefficients.

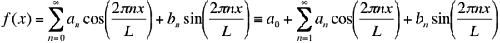
The computation of the (usual) Fourier series is based on the integral identities (see on-line Math Reference Data for more detail):


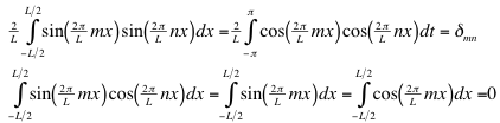
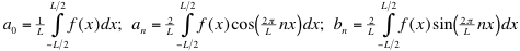
for m, n ≠ 0, where δmn = 1 if m = n and 0 otherwise is the Kronecker delta function. Since the cosine and sine functions form a complete orthogonal basis over the interval [−L/2, L/2], the Fourier coefficients are as follows:

Figures below illustrate steps of summation of sine waves to approach a square wave:
Images from the Math Reference Data http://math-reference.com/s_fourier.html
and http://www.brad.ac.uk/acad/lifesci/optometry/resources/modules/stage1//pvp1/CSF.html

With only one term, it is a simple sine wave, and adding the next terms brings the sum closer and closer to a square wave.

The Fourier series decomposition equally holds for 2D images, and the basis consists in this case of 2D sine and cosine functions. A Fourier series representation of a 2D function, f(x,y), having a period L in both the x and y directions is:


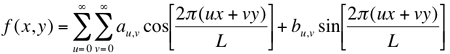
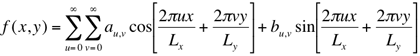
where u and v are the numbers of cycles fitting into one horizontal and vertical period, respectively, of f(x,y). In the general case, when both the periods are different (Lx and Ly, respectively) the Fourier series is quite similar:

The Fourier series representation of f(x,y) can be considered as a pair of 2D arrays of coefficients, each of infinite extent.

Return to the local table of contents

Discrete Fouirier transform

2D Fourier transform represents an image f(x,y) as the weighted sum of the basis 2D sinusoids such that the contribution made by any basis function to the image is determined by projecting f(x,y) onto that basis function. In digital image processing, each image function f(x,y) is defined over discrete instead of continuous domain, again finite or periodic. The use of sampled 2D images of finite extent leads to the following discrete Fourier transform (DFT) of an N×N image is:

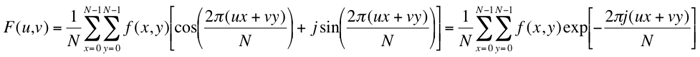
due to ejθ ≡ exp(jθ) = cos θ + jsin θ. The (forward) DFT results in a set of complex-valued Fourier coefficients F(u,v) specifying the contribution of the corresponding pair of basis images to a Fourier representation of the image. The term "Fourier transform" is applied either to the process of calculating all the values of F(u,v) or to the values themselves.

The inverse Fourier transform converting a set of Fourier coefficients into an image is very similar to the forward transform (except of the sign of the exponent):

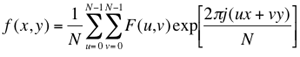
The forward transform of an N×N image yields an N×N array of Fourier coefficients that completely represent the original image (because the latter is reconstructed from them by the inverse transform). Manipulations with pixel values f(x,y) or Fourier coefficients F(u,v) are called processing in the spatial domain or frequency (spectral) domain, respectively. The transformation from one domain to another via a forward or inverse Fourier transform does not, in itself, cause any information loss.

Return to the local table of contents

Spectra and filtering

Real, R(u,v), and imaginary, I(u,v) parts of the complex number F(u,v) are not informative in themselves; more important representation is obtained by representing each complex coefficient F(u,v) with its magnitude, |F(u,v)|, and phase, φ(u,v):

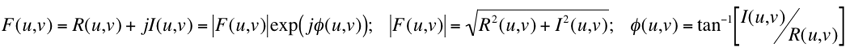
If an array of complex coefficients is decomposed into an array of magnitudes and an array of phases, the magnitudes correspond to the amplitudes of the basis images in the Fourier representation. The array of magnitudes is called the amplitude spectrum of the image, as well as the array of phases is called the phase spectrum. The power spectrum, or spectral density of an image is the squared amplitude spectrum: P(u,v) = |F(u,v)|2 = R2(u,v) + I2(u,v). All the power, amplitude, and phase spectra can be rendered as images themselves for visualisation and interpretation. While the amplitude spectrum reveals the presence of particular basis images in an image, the phase spectrum encodes their relative shifts. Thus, without phase information, the spatial coherence of the image is destroyed to such extent that it is impossible to recognise depicted objects. Without amplitude information, the relative brightnesses of these objects cannot be restored, although the boundaries between them can be found. Because phase is so important to keep the overall visuall appearance of an image, most of image processing operations in the frequency domain do not alter the phase spectrum and manipulate only the amplitude spectrum.

Properties of the Fourier transform

The basic properties of the DFT of an image are its periodicity and complex conjugate symmetry. The spectrum repeats itself endlessly in both directions with period N, i.e. F(u,v) = F(u + kN, v + lN) where k, l ∈ [−∞, ..., −1, 0, 1, 2,..., ∞]. The N×N block of the Fourier coiefficients F(u,v) computed from an N×N image with the 2D DFT is a single period from this infinite sequence. The second property arises because the image is real-valued whereas the DFT operates on complex numbers. Complex conjugate symmetry means that |F(u,v)| = |F(−u,−v)|, so that there exist negative frequencies which are mirror images of the corresponding positive frequencies as regarding the amplitude spectrum.

Due to periodicity and conjugate symmetry, the computed spectra have one peculiarity: for the computed values of F(u,v), frequency increases up to u = N/2 and decreases thereafter; the half of the spectrum for which u > N/2 is a "double reflection" of the half with u ≤ N/2, and the same applies to frequencies either side of v = N/2, as illustrated below:

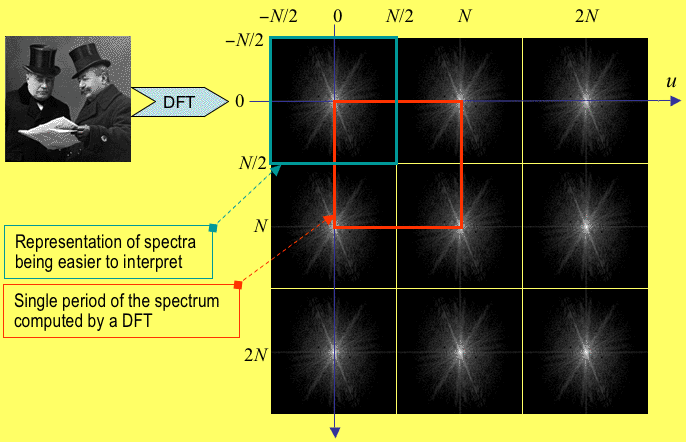
A portion of an infinite, periodic spectrum exhibiting complex conjugate symmetry,
and the sample of the spectrum being computed by the DFT.

The interpretation of spectra is made much easier if the results of the DFT are centred on the point (u = 0, v = 0), such that frequency increases in any direction away from the origin. This can be done by circular shifting of the four quadrants of the array or computing the DFT sums from −N/2 to N/2 rather than from 0 to N. Alternatively, by the shift theorem of the Fourier transform (see Wikipedia for a brief description of the shift theorem), the same result can be achieved by making the adjacent input values positive and negative by multiplying f(x,y) by (−1)x+y (i.e. by keeping the input values positive and negative for even and odd sums x+y, respectively). Typically, all the spectra are represented with the centre point as the origin to see and analyse dominant image frequencies. Because the lower frequency amplitudes mostly dominate over the mid-range and high-frequency ones, the fine structure of the amplitude spectrum can be perceived only after a non-linear mapping to the greyscale range [0, 255]. Among a host of possible ways, commonly used methods include a truncated linear amplitude mapping with the scale factor λ for the amplitude (the scaled amplitudes λa are cut out above the level 255; it is a conventional linear mapping if the maximum amplitude amax ≤ 255/λ) or the like truncated linear mapping after some continuous non-linear, e.g. logarithmic amplitude transformation. The examples below show amplitude spectra of the same image obtained with the linear or truncated linear mapping of the initial amplitudes and the logarithms of amplitudes:

Original image Amplitude spectrum: linear scale λ = 3.92 Truncated linear mapping λ = 15.7 Truncated linear mapping λ = 250.9
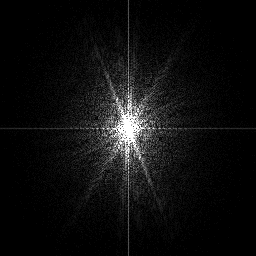
Phase spectrum Log-amplitude spectrum: linear scale λ = 60.9 Truncated log-linear mapping λ = 243.6 Truncated log-linear mapping λ = 487.2

Spectra of simple periodic patterns, e.g. of pure 2D sinusoidal patterns, are the simplest possible because correspond to a single basis image:

2D sinusoid Amplitude spectrum
Other pairs of simple images below (left) and their amplitude Fourier spectra (right) are taken from the webpage ket.dyndns.org/~durandal/public/:
   
Circle Square
   
Periodic circles Periodic squares

Images below demostrate the natural digital photo, its power, amplitude, and phase spectra, and the images reconstructed with the inverse DFT from the spectrum restricted to only higher or only lower frequencies ( these images are taken from www.aitech.ac.jp/~iiyoshi/ugstudy/ugst.html):

Original image Power spectrum Amplitude spectrum
Phase spectrum High-pass filtering Low-pass filtering

For a more detailed analysis of Fourier transform and other examples of 2D image spectra and filtering, see introductory materials prepared by Dr. John M. Brayer ( Professor Emeritus, Department of Computer Science, University of New Mexico, Albuquerque, New Mexico, USA).

Windowing

Fourier theory assumes that not only the Fourier spectrum is periodic but also the input DFT data array is a single period of an infinite image repeating itself infinitely in both directions:


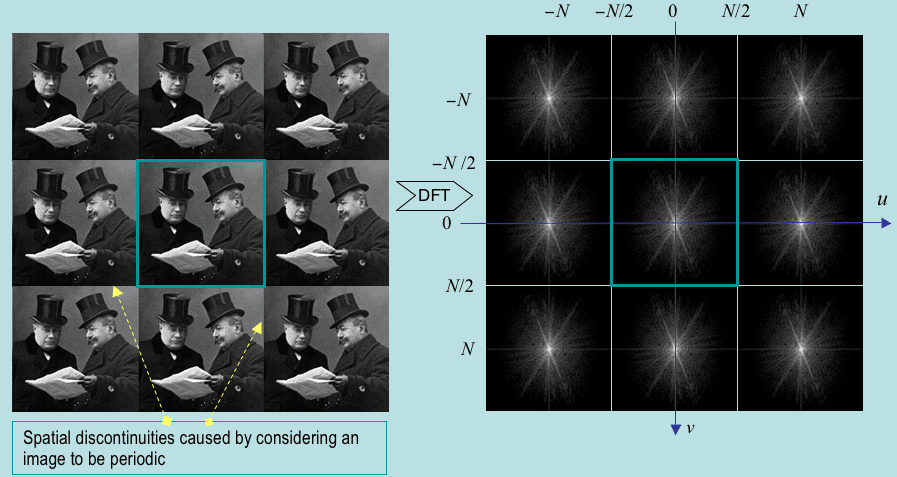
Equivalently, the image may be considered on a torus, i.e. wrapped around itself, so that the left and right sides and the top and bottom coincide. Any mismatch along these coinciding lines, i.e. any discontinuity in the periodic image, distort the Fourier spectrum. But this problem is minimised by windowing the images prior to the DFT in such a way as to gradually reduce the pixel values to zero at the edges of the image. The reduction is performed with a windowing function depending on the distance r of each image pixel (x,y) from the centre (xc,yc) of the image, r2 = (x − xc)2 + (y − yc)2, and a given maximum distance rmax. There are several standard windows such as:
After applying the Hanning window Truncated log-amplitude spectrum: λ = 352.8 Phase spectrum

Fast Fourier transform (FFT)

Computation of a single value of F(u,v) involves a summation over all image pixels, i.e. O(N2) operations if the image dimensions are N×N (recall the Big-Oh notation from COMPSCI 220). Thus, the overall complexity of a DFT calculating the spectrum with N2 values of F(u,v) is O(N4). Such algorithm is impractical: e.g. more than one hour or 12 days for the DFT of a 256×256 or 1024×1024 image, respectively, assuming one microsecond per multiplication of a complex number.

Due to the separability of the DFT, a 1D DFT can be performed along each image row to form an intermediate N×N array. Then a 1D DFT is performed down each column of this array in order to produce the desired N×N array of the values of F(u,v). In such a way the complexity of a 2D DFT is reduced from O(N4) to O(N3). But the cubic complexity is still too high to make the algorithm practicable.

Fortunately, there exists a fast Fourier transform (FFT) algorithm that computes a 1D Fourier transform for N points in only O(N log N) operations which makes FFT a practical and important operation on computers. The 1D FFT speeds up calculations due to a possibility to represent a Fourier transform of length N being a power of two in a recursive form, namely, as the sum of two Fourier transforms of length N/2. The recursion ends at the point of computing simple transforms of length 2. Then the overall complexity of this 1D FFT is proportional to N log2N, i.e. O(N log N) compared with O(N2) for a directly calculated 1D DFT. Therefore the complexity of the separable 2D FFT becomes O(N2 log N). For a 512×512 image, a 2D FFT is roughly 30,000 times faster than direct DFT.

An example of the 1D FFT program will highlight the simplicity of this recursive computation. The classic 2D FFT requires that both image dimensions are powers of two. There exist more complex FFT algorithms that allow for less restricted dimensions. Otherwise the image can be either cropped or padded out with zero pixel values to the appropriate dimensions. The former approach discards data and may distort the spectrum but reduces processing time, while the latter increases time but does not affect the spectrum.

Filtering of images

Filtering in the spatial domain is performed by convolution with an appropriate kernel. This operation impacts spatial frequencies but it is difficult to quantify this impact in the spatial domain. The spectral (frequency) domain is more natural to specify these effects; also filtering in the spectral domain is computationally simpler because convolution in the spatial domain is replaced with the point-to-point multiplication of the complex image spectrum by a filter transfer function.

Let F, H, and G denote the spectrum of the image f, the filter transfer function (i.e. the spectrum of the convolution kernel h), and the spectrum of the filtered image g, respectively. Then the convolution theorem states that f∗h ⇔ G(u,v) = F(u,v)H(u,v) (the derivation takes into account that the image is infinite and periodic with the period N in the both directions; the sign "⇔" indicates a Fourier transform pair such that each its side is converted into the opposite one by a Fourier transform, i.e. the left-to-right forward and right-to-left inverse transforms):


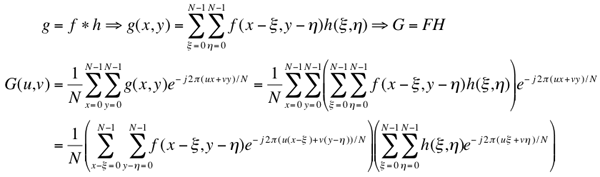
The filtered image g can be computed using the inverse DFT. Generally, filtering in the spectral domain impacts both the amplitude and phase of the image spectrum F(u,v). In practice, most filters do not affect phases and change only magnitudes, i.e. they are zero-phase-shift filters.

Convolving an image with a certain kernel has the same effect on that image as multiplying the spectrum of that image by the Fourier transform of the kernel. Therefore, linear filtering can always be performed either in the spatial or the spectral domains.

A low pass filtering suppresses high frequency components and produces smoothed images. An ideal sharp cut-off filter simply blocks all frequencies at distances larger than a fixed filter radius r0 from the centre (0,0) of the spectrum:

H(u,v) = 1 if r(u,v) ≤ r0 and H(u,v) = 0 if r(u,v) > r0

where r(u,v) = [u2 + v2]1/2 is the distance form the centre of the spectrum. But such a filter produces a rippled effect around the image edges because the inverse DFT of such a filter is a "sinc function", sin(r)/r. To avoid ringing, a low pass transfer function should smoothly fall to zero. One of most known filters of such type is the Butterworth low pass filter of order n: H(u,v) = 1/(1 + [r(u,v)/r0]2n) where the value r0 defines the distance at which H(u,v) = 0.5 rather than the cut-off radius. When the order increases, the Butterworth filter approaches the ideal low pass filter. Many other transfer functions perform low pass filtering. An important example of a smooth and well-behaved spectral filter is a Gaussian transfer function (its Fourier transform results in another Gaussian).

A high pass filtering suppresses low frequency components and produces images with enhanced edges. An ideal high pass filter suppresses all frequencies up to the cutoff one and does not change frequencies beyond this border:

H(u,v) = 0 if r(u,v) ≤ r0 and H(u,v) = 1 if r(u,v) > r0

Just as the ideal low pass filter, it leads to ringing in the filtered image. This effect is avoided by using a smoother filter, e.g. the Butterworth high pass filter of order n with the transfer function H(u,v) = 1/(1 + [r0/r(u,v)]2n). Both the high-pass and the low pass Butterworth filters approach the ideal cutoff ones if the filtert order increases.

A band pass filtering preserves a certain range of frequencies and suppress all others. Conversely, a band stop filtering suppresses a range of frequencies and preserves all other frequencies. For example, a band stop filter may combine a low pass filter of radius rlow and a high pass filter of radius rhigh, with rlow > rhigh. The transfer function of a Butterworth band stop filter with radius r0 = (rlow + rhigh)/2 and the band width Δ = rhigh − rlow is specified as Hs = 1 / (1 + [Δr(u,v)/(r2(u,v) − r02)]2n) where r(u,v) = [u2 + v2]1/2. The corresponding band pass filter is Hp = 1 − Hs. Even more versatile filtering is produced by selective editing of specific frequencies, in particular, the removal of periodic sinusoidal noise by suppressing narrow spikes in the spectrum.

Return to the local table of contents

Convolution and deconvolution

Additive random noise caused by an imaging device is not the only source of image degradation. For example, image blurring might be induced by the poor lens focusing, object movements, and / or atmospheric turbulence. A conventional model of the degraded image assumes that a perfect image f is blurred by filtering with a certain convolution kernel h and further corrupted by the addition of noise ε:


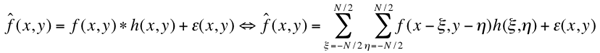
The convolution kernel h, which models the blurring caused by all degradation sources in the scene and imaging device, is called the point spread function (PSF). Generally, both h and ε may vary spatially, but usually the model is simplified by assuming that the degradation h is spatially invariant. The PSF specifies how a point source is impacted by the imaging process. The perfect process forms for a point source an image with a single bright point and other zero-valued pixels, while the real process produces an area of non-zero pixels such that a grey level profile across this area follows the PSF. To deconvolve an image, its PSF has to be known or estimated from measurements of the image.

The way to inverting the convolution is clearer in the spectral domain: in accord with the convolution theorem, the spectra of the perfect and degraded images, noise spectrum E, and DFT of the PSF, called the modulation transfer function (MTF) relate as follows:


Assuming the noise is negligible, the simplest deconvolution to restore an initial (perfect) image from the degraded one is based on inverse filtering:

where 1/H(u,v) is the inverse filter to remove the degradation. But in practice this approach encounters numerous problems, first, with zeros of the MTF (that result in indeterminate or infinite ratios), and secondly, with noisy data when the term E(u,v)/H(u,v) may become large and dominate F(u,v) which should be recovered. Empirical solutions to these problems set a threshold on H(u,v) below which the corresponding values of F(u,v) are set to zero and limit inverse filtering to a certain distance from the origin of the spectrum. In some cases these heuristics are sufficient to clearly improve the output (restored) image over the input (degraded) one.

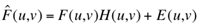
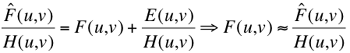
A more theoretically justified solution is the Wiener filtering that minimises the expected squared error between the restored and perfect images. A simplified Wiener filter is as follows:


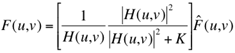
where K is a constant value directly proportional to the variance of the noise present in the image and inversely proportional to the variance of the image with respect to the average grey value. If K = 0 (no noise), the Wiener filter reduces to a simple inverse filter. If K is large compared with |H(u,v)|, then the large value of the inverse filtering term 1/H(u,v) is balanced out with the small value of the second term inside the brackets.

Return to the local table of contents

References

These lecture notes follow Chapter 8 "The Frequency Domain" of the textbook

with extra examples and teaching materials taken mostly, with corresponding references, from the Web. In addition to further reading proposed in Section 8.7 of the textbook, many other image processing texts discuss and explain Fourier transforms and their applications to image filtering, e.g.

Return to the local table of contents

Return to the general table of contents