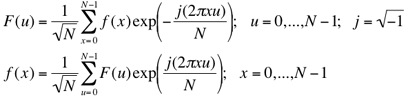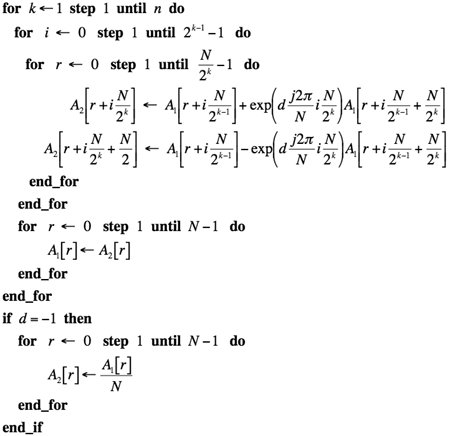Fast Fourier Transform: A Simple Program

This quite short FFT program implements an algorithm published almost 40 years ago by M. L. Ulrich, "FFT's without sorting", IEEE Transactions on Acoustics and Electroacoustics, vol. AU-17, no. 2, 1969, pp. 170 - 172. Originally it was written on an old programming language Fortran. This is why below it is rewritten on C using a special structure for complex numbers and a few utilities to manipulate with complex numbers. You may easily rewrtite it on Java. 

#define COMPLEX struct complex_type
COMPLEX {
  double real; /* real part of the complex number real + sqrt(-1)*imag */
  double imag; /* imaginary part of the complex number */
};

#define PI2 6.2831853

void fft1d( COMPLEX *fftarray, int narray, int direction ){
/*
*  Fast Fourier Transform of a 1D complex data array of size narray
*     (narray is a power of two number, i.e. narray = 2^nstage
*  ------------------------------------------------------------------
*  fftarray[ 2*narray] - working complex array of input/output data
*  direction = +1 or -1 for the inverse and forward FFT, respectively
*
*  Input for the direct and inverse FFT, output for the inverse FFT 
*     and unnormalised output for the forward FFT : in the first half  
*     of the working array: fftarray[0]...fftarray[narray-1]
*  Normalised output for the forward FFT: in the second half of the 
*           working array: fftarray[narray]...fftarray[2*narray-1] 
*  ------------------------------------------------------------------
*/
   int     i, in2k, ir, isub, isub1, isub2, isub3, k, k2k;  
   int     n2k, n2array, ni, nstage;
   double  pi2n, temp;
   COMPLEX w, prod;

   nstage = (int)log2( (double)narray );
   pi2n = PI2 * (double)direction / (double)narray;
   n2array = narray / 2;

   for( k = 1, k2k = 2; k <= nstage; k++, k2k *= 2 ) {
     n2k = narray / k2k;
     ni = k2k / 2;
     for( i = 0; i < ni; i++ ) {
       in2k = i * n2k;
	   temp = (double)in2k * pi2n;
	   w.real = cos( temp );
	   w.imag = sin( temp );
	   for( ir = 0; ir < n2k; ir++ ){
	     isub  = ir    + in2k;
	     isub1 = ir    + in2k * 2;
	     isub2 = isub1 + n2k;
	     isub3 = isub  + n2array;
		 prod = multiply_complex( w, fftarray[ isub2 ] );
		 fftarray[ isub  + narray ] = add_complex( fftarray[ isub1 ], prod );
		 fftarray[ isub3 + narray ] = subtract_complex( fftarray[ isub1 ], prod );
	   }
     }
     for( ir = 0; ir < narray; ir++ ) {
	   fftarray[ ir ] = copy_complex( fftarray[ ir + narray ] );
     }
   }
   for( ir = 0; ir < narray; ir++ ) {
     fftarray[ ir + narray ] = scale_complex( fftarray[ ir ], (double)narray );
   }
} 

/*===================== Utilities ===============================================*/

COMPLEX copy_complex( COMPLEX var ){
/*
*  assign one complex value var to another variable
*/
   COMPLEX new;

   new.real = var.real;
   new.imag = var.imag;
   return new;
}

COMPLEX scale_complex( COMPLEX var, double scale ){
/*
*  divide a complex value var by real scale
*/
   COMPLEX new;

   new.real = var.real / scale;
   new.imag = var.imag / scale;
   return new;
}

COMPLEX multiply_complex( COMPLEX var1, COMPLEX var2 ){
/*
*  multiply a complex value var1 to another value var2
*/
   COMPLEX product;
  
   product.real = var1.real * var2.real - var1.imag * var2.imag;
   product.imag = var1.real * var2.imag + var1.imag * var2.real;
   return product;
}

COMPLEX add_complex( COMPLEX var1, COMPLEX var2 ){
/*
*  sum complex values var1 and var2
*/
   COMPLEX sum;

   sum.real = var1.real + var2.real;  
   sum.imag = var1.imag + var2.imag;
   return sum;  
}

COMPLEX subtract_complex( COMPLEX var1, COMPLEX var2 ){
/*
*  subtract a complex value var2 from var1
*/
   COMPLEX diff;

   diff.real = var1.real - var2.real;  
   diff.imag = var1.imag - var2.imag;
   return diff;  
}

This FFT algorithm assumes that the size of input data is a power of two: N = 2n (the values N and n are represented with the program variables narray and nstage, respectively. Here, the forward and inverse FFT of the complex input data differ only by the sign of the exponent ("−" for the forward and "+" for the inverse FFT, respectively, and by normalisation of only the forward FFT output:


To symmetrise the normalisation (just as it was done for the 2D FFT), both the forward and inverse transforms can be normalised as follows (with obvious changes in the above program):

The program uses the working complex array fftarray of size 2N to store both the input, intermediate, and output data. The block-diagram of the program is given below (here, d is the sign factor named direction in the program, and the arrays A1 and A2 denote the first and second halves of the working array fftarray, respectively):