Data Structures and Algorithms: Red-Black Trees

Data Structures and Algorithms

8.2 Red-Black Trees

A red-black tree is a binary search tree with one extra attribute for each node: the colour, which is either red or black. We also need to keep track of the parent of each node, so that a red-black tree's node structure would be:

struct t_red_black_node {
    enum { red, black } colour;
    void *item;
    struct t_red_black_node *left,
                     *right,
                     *parent;
    }

For the purpose of this discussion, the NULL nodes which terminate the tree are considered to be the leaves and are coloured black.

Definition of a red-black tree

A red-black tree is a binary search tree which has the following red-black properties:

Every node is either red or black.
Every leaf (NULL) is black.
If a node is red, then both its children are black.
Every simple path from a node to a descendant leaf contains the same number of black nodes.

implies that on any path from the root to a leaf, red nodes must not be adjacent.
However, any number of black nodes may appear in a sequence.

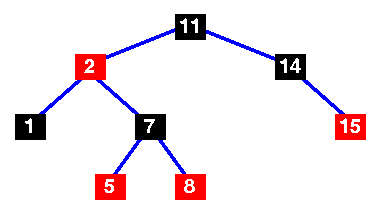
	A basic red-black tree
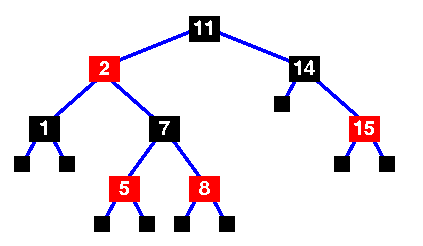
	Basic red-black tree with the sentinel nodes added. Implementations of the red-black tree algorithms will usually include the sentinel nodes as a convenient means of flagging that you have reached a leaf node. They are the NULL black nodes of property 2.

The number of black nodes on any path from, but not including, a node x to a leaf is called the black-height of a node, denoted bh(x). We can prove the following lemma:

Lemma

A red-black tree with n internal nodes has height at most 2log(n+1).
(For a proof, see Cormen, p 264)

This demonstrates why the red-black tree is a good search tree: it can always be searched in O(log n) time.

As with heaps, additions and deletions from red-black trees destroy the red-black property, so we need to restore it. To do this we need to look at some operations on red-black trees.

Rotations

A rotation is a local operation in a search tree that preserves in-order traversal key ordering.

Note that in both trees, an in-order traversal yields:

A x B y C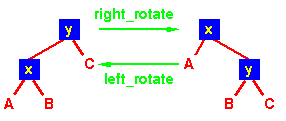

The left_rotate operation may be encoded:

left_rotate( Tree T, node x ) {
    node y;
    y = x->right;
    /* Turn y's left sub-tree into x's right sub-tree */
    x->right = y->left;
    if ( y->left != NULL )
        y->left->parent = x;
    /* y's new parent was x's parent */
    y->parent = x->parent;
    /* Set the parent to point to y instead of x */
    /* First see whether we're at the root */
    if ( x->parent == NULL ) T->root = y;
    else
        if ( x == (x->parent)->left )
            /* x was on the left of its parent */
            x->parent->left = y;
        else
            /* x must have been on the right */
            x->parent->right = y;
    /* Finally, put x on y's left */
    y->left = x;
    x->parent = y;
    }

Insertion

Insertion is somewhat complex and involves a number of cases. Note that we start by inserting the new node, x, in the tree just as we would for any other binary tree, using the tree_insert function. This new node is labelled red, and possibly destroys the red-black property. The main loop moves up the tree, restoring the red-black property.

rb_insert( Tree T, node x ) {
    /* Insert in the tree in the usual way */
    tree_insert( T, x );
    /* Now restore the red-black property */
    x->colour = red;
    while ( (x != T->root) && (x->parent->colour == red) ) {
       if ( x->parent == x->parent->parent->left ) {
           /* If x's parent is a left, y is x's right 'uncle' */
           y = x->parent->parent->right;
           if ( y->colour == red ) {
               /* case 1 - change the colours */
               x->parent->colour = black;
               y->colour = black;
               x->parent->parent->colour = red;
               /* Move x up the tree */
               x = x->parent->parent;
               }
           else {
               /* y is a black node */
               if ( x == x->parent->right ) {
                   /* and x is to the right */ 
                   /* case 2 - move x up and rotate */
                   x = x->parent;
                   left_rotate( T, x );
                   }
               /* case 3 */
               x->parent->colour = black;
               x->parent->parent->colour = red;
               right_rotate( T, x->parent->parent );
               }
           }
       else {
           /* repeat the "if" part with right and left
              exchanged */
           }
       }
    /* Colour the root black */
    T->root->colour = black;
    }

Here's an example of the insertion operation.

Animation

Red-Black Tree Animation
This animation was written by Linda Luo, Mervyn Ng, Anita Lee, John Morris and Woi Ang.

Please email comments to:

Examination of the code reveals only one loop. In that loop, the node at the root of the sub-tree whose red-black property we are trying to restore, x, may be moved up the tree at least one level in each iteration of the loop. Since the tree originally has O(log n) height, there are O(log n) iterations. The tree_insert routine also has O(log n) complexity, so overall the rb_insert routine also has O(log n) complexity.

Key terms

Red-black trees: Trees which remain balanced - and thus guarantee O(logn) search times - in a dynamic environment. Or more importantly, since any tree can be re-balanced - but at considerable cost - can be re-balanced in O(logn) time.