| Data Structures and Algorithms |
| 8.3.3 Hashing Functions |
Choosing a good hashing function, h(k), is essential for hash-table based searching. h should distribute the elements of our collection as uniformly as possible to the "slots" of the hash table. The key criterion is that there should be a minimum number of collisions.
If the probability that a key, k, occurs in our collection is P(k), then if there are m slots in our hash table, a uniform hashing function, h(k), would ensure:
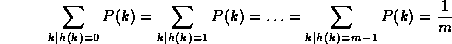
Sometimes, this is easy to ensure. For example, if the keys are randomly distributed in (0,r], then,
will provide uniform hashing.
Having mapped the keys to a set of natural numbers, we then have a number of possibilities.
h(k) = k mod m.
When using this method, we usually avoid certain values of m. Powers of 2 are usually avoided, for k mod 2b simply selects the b low order bits of k. Unless we know that all the 2b possible values of the lower order bits are equally likely, this will not be a good choice, because some bits of the key are not used in the hash function.
Prime numbers which are close to powers of 2 seem to be generally good choices for m.
For example, if we have 4000 elements, and we have chosen an overflow table organization, but wish to have the probability of collisions quite low, then we might choose m = 4093. (4093 is the largest prime less than 4096 = 212.)
Thus the hash function is:
In this case, the value of m is not critical and we typically choose a power of 2 so that we can get the following efficient procedure on most digital computers:
It seems that:
is a good choice (see Knuth, "Sorting and Searching", v. 3 of "The Art of Computer Programming").
A malicious adversary can always chose the keys so that they all hash to the same slot, leading to an average O(n) retrieval time. Universal hashing seeks to avoid this by choosing the hashing function randomly from a collection of hash functions (cf Cormen et al, p 229- ). This makes the probability that the hash function will generate poor behaviour small and produces good average performance.
Key terms |
| Continue on to Dynamic Algorithms | Back to the Table of Contents |
 , 1998
, 1998