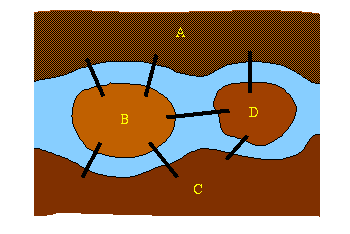
The puzzle asks whether it is possible to take a tour through the park, crossing each bridge only once.
| Data Structures and Algorithms |
| 13 Hard or Intractable Problems |
If a problem has an O(nk) time algorithm (where k is a constant), then we class it as having polynomial time complexity and as being efficiently solvable.
If there is no known polynomial time algorithm, then the problem is classed as intractable.
The dividing line is not always obvious. Consider two apparently similar problems:
| Euler's problem (often characterized as the Bridges of Königsberg - a popular 18th C puzzle) |
asks whether there is a path through a graph which traverses each edge only once. |
| Hamilton's problem | asks whether there is a path through a graph which visits each vertex exactly once. |
 |
The 18th century German city of Königsberg was situated on the river Pregel.
Within a park built on the banks of the river, there were two islands joined by seven
bridges.
The puzzle asks whether it is possible to take a tour through the park, crossing each bridge only once. |
An exhaustive search requires starting at every possible point and traversing all the possible paths from that point - an O(n!) problem. However Euler showed that an Eulerian path existed iff
|
the nodes represent the "dry land" points and the arcs represent the bridges. 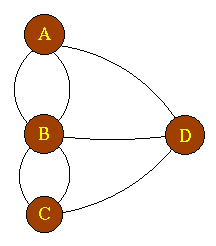 |
We can now easily see that the Bridges of Königsberg does not have a solution. A quick inspection shows that it does have a Hamiltonian path. |
However there is no known efficient algorithm for determining whether a Hamiltonian path exists.But if a path was found, then it can be verified to be a solution in polynomial time: we simply verify that each edge in the path is actually an edge (O(e) if the edges are stored in an adjacency matrix) and that each vertex is visited only once (O(n2) in the worst case).
|
Euler's problem lies in the class P:
problems solvable in Polynomial time.
Hamilton's problem is believed
to lie in class NP (Non-deterministic Polynomial).
Note that I wrote "believed" in the previous sentence. No-one has succeeded in proving that efficient (ie polynomial time) algorithms don't exist yet! |
What does NP mean?At each step in the algorithm, you guess which possibility to try next. This is the non-deterministic part: it doesn't matter which possibility you try next. There is no information used from previous attempts (other than not trying something that you've already tried) to determine which alternative should be tried next. However, having made a guess, you can determine in polynomial time whether it is a solution or not.Since nothing from previous trials helps you to determine which alternative should be tried next, you are forced to investigate all possibilities to find a solution. So the only systematic thing you can do is use some strategy for systematically working through all possibilities, eg setting out all permutations of the cities for the travelling salesman's tour. |
Many other problems lie in class NP. Some examples follow.
a1 op a2 op ... op anwhere op are boolean operators, and, or, ..
Can we find an assignment of (true,false) to the ai so that the expression is true? This problem is equivalent to the circuit-satisfiability problem which asks can we find a set of inputs which will produce a true at the output of a circuit composed of arbitrary logic gates.
A solution can only be found by trying all 2n possible assignments.
|
The three-colour map colouring problem asks if we can colour a map so that no
adjoining countries have the same colour.
Once a solution has been guessed, then it is
readily proved.
[This problem is easily answered if there are only 2 colours - there must be no point at which an odd number of countries meet - or 4 colours - there is a proof that 4 colours suffice for any map.] |
 |
This problem has a graph equivalent: each vertex represents a country and an edge is drawn between two vertices if they share a common border.
Its solution has a more general application. If we are scheduling work in a factory: each vertex can represent a task to be performed - they are linked by an edge if they share a common resource, eg require a particular machine. A colouring of the vertices with 3 colours then provides a 3-shift schedule for the factory.
Many problems are reducible to others: map colouring can be reduced to graph colouring. A solution to a graph colouring problem is effectively a solution to the equivalent map colouring or scheduling problem. The map or graph-colouring problem may be reduced to the boolean satisfiability problem. To give an informal description of this process, assume the three colours are red, blue and green. Denote the partial solution, "A is red" by ar so that we have a set of boolean variables:
| ar | A is red | ab | A is blue | ag | A is green | br | B is red | bb | B is blue | bg | B is green | cr | C is red | ... | ... |
Now a solution to the problem may be found by finding values for ar, ab, etc which make the expression true:
((ar and not ab and not ag) and ( (bb and (cb and (dg ....
Thus solving the map colouring problem is equivalent to finding an assignment to the variables which results in a true value for the expression - the boolean satisfiability problem.
There is a special class of problems in NP: the NP-complete problems. All the problems in NP are efficiently reducible to them. By efficiently, we mean in polynomial time, so the term polynomially reducible provides a more precise definition.
In 1971, Cook was able to prove that the boolean satisfiability problem was NP-complete. Proofs now exist showing that many problems in NP are efficiently reducible to the satisfiability problem. Thus we have a large class of problems which will are all related to each other: finding an efficient solution to one will result in an efficient solution for them all.
An efficient solution has so far eluded a very large number of researchers but there is also no proof that these problems cannot be solved in polynomial time, so the search continues.
Class NP problems are solvable by non-deterministic algorithms: these algorithms consist of deterministic steps alternating with non-deterministic steps in which a random choice (a guess) must be made. A deterministic algorithm must, given a possible solution,
We can also view this from the other aspect: that of trying to determine a solution. At each guessing stage, the algorithm randomly selects another element to add to the solution set: this is basically building up a "game" tree. Various techniques exist for pruning the tree - backtracking when an invalid solution is found and trying another branch, but this is where the exponential time complexity starts to enter!
Can we find a tour with a cost less than x?
By asking this question until we find a tour with a cost x for which the answer is provably no, we have found the optimal tour. This problem can also be proved to be in NP. (It is reducible to the Hamiltonian circuit problem.)
Various heuristics have been developed to find near optimal solutions with efficient algorithms.
One simple approach is the find the minimum spanning tree. One possible tour simple traverses the MST twice. So we can find a tour which is at most twice as long as the optimum tour in polynomial time. Various heuristics can now be applied to reduce this tour, eg by taking shortcuts.
An algorithm due to Christofides can be shown to produce a tour which is no more than 50% longer than the optimal tour.
 |
It starts with the MST and singles out all cities
which are linked to an odd number of cities. These are linked in pairs by a variant of the procedure used to find compatible room-mates. |
 |
This can then be improved by taking shortcuts. |
Another strategy which works well in practice is to divide the "map" into many small regions and to generate the optimum tour by exhaustive search within those small regions. A greedy algorithm can then be used to link the regions. While this algorithm will produce tours as little as 5% longer than the optimum tour in acceptable times, it is still not guaranteed to produce the optimal solution.
Key terms |
| Continue on to Games | Back to the Table of Contents |
 , 1998
, 1998