The compute engine is a relatively simple program: it runs tasks that are handed to it. The clients for the compute engine are more complex. A client needs to call the compute engine, but it also has to define the task to be performed by the compute engine.

Two separate classes make up the client in our example. The first class, ComputePi, looks up and invokes a Compute object. The second class, Pi, implements the Task interface and defines the work to be done by the compute engine. The job of the Pi class is to compute the value of to some number of decimal places.

The non-remote Task interface is defined as follows:

package compute;

public interface Task<T> {
    T execute();
}

The code that invokes a Compute object's methods must obtain a reference to that object, create a Task object, and then request that the task be executed. The definition of the task class Pi is shown later. A Pi object is constructed with a single argument, the desired precision of the result. The result of the task execution is a java.math.BigDecimal representing calculated to the specified precision.

Here is the source code for client.ComputePi, the main client class:

package client;

import java.rmi.registry.LocateRegistry;
import java.rmi.registry.Registry;
import java.math.BigDecimal;
import compute.Compute;

public class ComputePi {
    public static void main(String args[]) {
        if (System.getSecurityManager() == null) {
            System.setSecurityManager(new SecurityManager());
        }
        try {
            String name = "Compute";
            Registry registry = LocateRegistry.getRegistry(args[0]);
            Compute comp = (Compute) registry.lookup(name);
            Pi task = new Pi(Integer.parseInt(args[1]));
            BigDecimal pi = comp.executeTask(task);
            System.out.println(pi);
        } catch (Exception e) {
            System.err.println("ComputePi exception:");
            e.printStackTrace();
        }
    }    
}

Like the ComputeEngine server, the client begins by installing a security manager. This step is necessary because the process of receiving the server remote object's stub could require downloading class definitions from the server. For RMI to download classes, a security manager must be in force.

After installing a security manager, the client constructs a name to use to look up a Compute remote object, using the same name used by ComputeEngine to bind its remote object. Also, the client uses the LocateRegistry.getRegistry API to synthesize a remote reference to the registry on the server's host. The value of the first command-line argument, args[0], is the name of the remote host on which the Compute object runs. The client then invokes the lookup method on the registry to look up the remote object by name in the server host's registry. The particular overload of LocateRegistry.getRegistry used, which has a single String parameter, returns a reference to a registry at the named host and the default registry port, 1099. You must use an overload that has an int parameter if the registry is created on a port other than 1099.

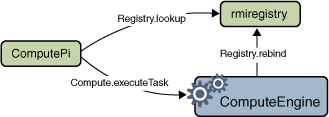
Next, the client creates a new Pi object, passing to the Pi constructor the value of the second command-line argument, args[1], parsed as an integer. This argument indicates the number of decimal places to use in the calculation. Finally, the client invokes the executeTask method of the Compute remote object. The object passed into the executeTask invocation returns an object of type BigDecimal, which the program stores in the variable result. Finally, the program prints the result. The following figure depicts the flow of messages among the ComputePi client, the rmiregistry, and the ComputeEngine.

The Pi class implements the Task interface and computes the value of to a specified number of decimal places. For this example, the actual algorithm is unimportant. What is important is that the algorithm is computationally expensive, meaning that you would want to have it executed on a capable server.

Here is the source code for client.Pi, the class that implements the Task interface:

package client;

import compute.Task;
import java.io.Serializable;
import java.math.BigDecimal;

public class Pi implements Task<BigDecimal>, Serializable {

    private static final long serialVersionUID = 227L;

    /** constants used in pi computation */
    private static final BigDecimal FOUR =
        BigDecimal.valueOf(4);

    /** rounding mode to use during pi computation */
    private static final int roundingMode = 
        BigDecimal.ROUND_HALF_EVEN;

    /** digits of precision after the decimal point */
    private final int digits;
    
    /**
     * Construct a task to calculate pi to the specified
     * precision.
     */
    public Pi(int digits) {
        this.digits = digits;
    }

    /**
     * Calculate pi.
     */
    public BigDecimal execute() {
        return computePi(digits);
    }

    /**
     * Compute the value of pi to the specified number of 
     * digits after the decimal point.  The value is 
     * computed using Machin's formula:
     *
     *          pi/4 = 4*arctan(1/5) - arctan(1/239)
     *
     * and a power series expansion of arctan(x) to 
     * sufficient precision.
     */
    public static BigDecimal computePi(int digits) {
        int scale = digits + 5;
        BigDecimal arctan1_5 = arctan(5, scale);
        BigDecimal arctan1_239 = arctan(239, scale);
        BigDecimal pi = arctan1_5.multiply(FOUR).subtract(
                                  arctan1_239).multiply(FOUR);
        return pi.setScale(digits, 
                           BigDecimal.ROUND_HALF_UP);
    }
    /**
     * Compute the value, in radians, of the arctangent of 
     * the inverse of the supplied integer to the specified
     * number of digits after the decimal point.  The value
     * is computed using the power series expansion for the
     * arc tangent:
     *
     * arctan(x) = x - (x^3)/3 + (x^5)/5 - (x^7)/7 + 
     *     (x^9)/9 ...
     */   
    public static BigDecimal arctan(int inverseX, 
                                    int scale) 
    {
        BigDecimal result, numer, term;
        BigDecimal invX = BigDecimal.valueOf(inverseX);
        BigDecimal invX2 = 
            BigDecimal.valueOf(inverseX * inverseX);

        numer = BigDecimal.ONE.divide(invX,
                                      scale, roundingMode);

        result = numer;
        int i = 1;
        do {
            numer = 
                numer.divide(invX2, scale, roundingMode);
            int denom = 2 * i + 1;
            term = 
                numer.divide(BigDecimal.valueOf(denom),
                             scale, roundingMode);
            if ((i % 2) != 0) {
                result = result.subtract(term);
            } else {
                result = result.add(term);
            }
            i++;
        } while (term.compareTo(BigDecimal.ZERO) != 0);
        return result;
    }
}

Note that all serializable classes, whether they implement the Serializable interface directly or indirectly, must declare a private static final field named serialVersionUID to guarantee serialization compatibility between versions. If no previous version of the class has been released, then the value of this field can be any long value, similar to the 227L used by Pi, as long as the value is used consistently in future versions. If a previous version of the class has been released without an explicit serialVersionUID declaration, but serialization compatibility with that version is important, then the default implicitly computed value for the previous version must be used for the value of the new version's explicit declaration. The serialver tool can be run against the previous version to determine the default computed value for it.

The most interesting feature of this example is that the Compute implementation object never needs the Pi class's definition until a Pi object is passed in as an argument to the executeTask method. At that point, the code for the class is loaded by RMI into the Compute object's Java virtual machine, the execute method is invoked, and the task's code is executed. The result, which in the case of the Pi task is a BigDecimal object, is handed back to the calling client, where it is used to print the result of the computation.

The fact that the supplied Task object computes the value of Pi is irrelevant to the ComputeEngine object. You could also implement a task that, for example, generates a random prime number by using a probabilistic algorithm. That task would also be computationally intensive and therefore a good candidate for passing to the ComputeEngine, but it would require very different code. This code could also be downloaded when the Task object is passed to a Compute object. In just the way that the algorithm for computing is brought in when needed, the code that generates the random prime number would be brought in when needed. The Compute object knows only that each object it receives implements the execute method. The Compute object does not know, and does not need to know, what the implementation does.