The Gentle Introduction To Haskell
back next
In this section we introduce the predefined standard type classes in Haskell. We have simplified these classes somewhat by omitting some of the less interesting methods in these classes; the Haskell report contains a more complete description. Also, some of the standard classes are part of the standard Haskell libraries; these are described in the Haskell Library Report.

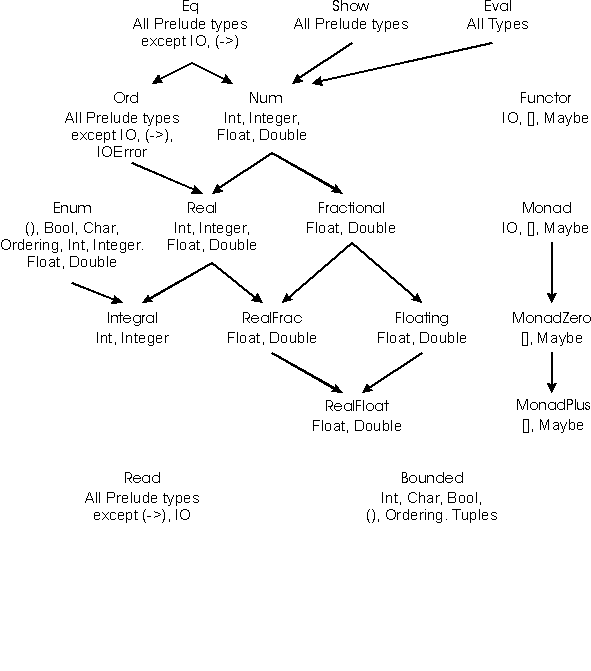
Haskell's standard classes form the somewhat imposing inclusion structure shown in Figure 3. At the top of the figure, we see Eq with its subclass Ord below it. These were defined in the previous section.
Class Enum has a set of operations that underlie the syntactic sugar of arithmetic sequences; for example, the arithmetic sequence expression [1,3..] stands for enumFromThen 1 3 (see §3.10 for the formal translation). We can now see that arithmetic sequence expressions can be used to generate lists of any type that is an instance of Enum. This includes not only most numeric types, but also Char, so that, for instance, ['a'..'z'] denotes the list of lower-case letters in alphabetical order. Furthermore, user-defined enumerated types like Color can easily be given Enum instance declarations. If so:
[Red..Violet] => [Red, Green, Blue, Indigo, Violet]
Note that such a sequence is arithmetic in the sense that the increment between values is constant, even though the values are not numbers. Most types in Enum can be mapped onto integers; for these, the fromEnum and toEnum convert between Int and a type in Enum.
The instances of class Show are those types that can be converted
to character strings (typically for I/O). The class Read
provides operations for parsing character strings to obtain the values
they may represent. As the primitive operations in these classes are
somewhat esoteric, let's begin with one of the higher-level functions that
is defined in terms of them:
show :: (Show a) => a -> String
Naturally enough, show takes any value of an appropriate type and
returns its representation as a character string (list of characters),
as in show (2+2), which results in "4". This is fine as far as
it goes, but we typically need to produce more complex strings
that may have the representations of many values in them, as in
"The sum of " ++ show x ++ " and " ++ show y ++ " is " ++ show (x+y) ++ "."
and after a while, all that concatenation gets to be a bit
inefficient. Specifically, let's consider a function to represent
the binary trees of Section 2.2.1 as a string,
with suitable markings to show the nesting of subtrees and the
separation of left and right branches (provided the element type is
representable as a string):
showTree :: (Show a) => Tree a -> String
showTree (Leaf x) = show x
showTree (Branch l r) = "<" ++ showTree l ++ "|" ++ showTree r ++ ">"
Because (++) has time complexity linear in the length of its
left argument, showTree is quadratic in the size of the tree.
To restore linear complexity, the function shows is provided:
shows :: (Show a) => a -> String -> String
shows takes a printable value and a string and returns
that string with the value's representation concatenated
at the front. The second argument serves as a sort of string
accumulator, and show can now be defined as shows with
the null accumulator:
show x = shows x ""
We can use shows to define a more efficient version of showTree,
which also has a string accumulator argument:
showsTree :: (Show a) => Tree a -> String -> String
showsTree (Leaf x) s = shows x s
showsTree (Branch l r) s= '<' : showsTree l ('|' : showsTree r ('>' : s))
This solves our efficiency problem (showsTree has linear complexity),
but the presentation of this function (and others like it) can be
improved. First, let's create a type synonym:
type ShowS = String -> String
This is the type of a function that returns a string representation of
something followed by an accumulator string.
Second, we can avoid carrying accumulators around, and also avoid
amassing parentheses at the right end of long constructions, by using
functional composition:
showsTree :: (Show a) => Tree a -> ShowS
showsTree (Leaf x) = shows x
showsTree (Branch l r) = ('<':) . showsTree l . ('|':) . showsTree r . ('>':)
Something more important than just tidying up the code has come about
by this transformation: We have raised the presentation from an
object level (in this case, strings) to a function level.
We can think of the typing as saying that showsTree maps a tree
into a showing function. Functions like ('<' :) or
("a string" ++) are primitive showing functions, and we build up
more complex functions by function composition.
Now that we can turn trees into strings, let's turn to the inverse
problem. The basic idea is a parser for a type a, which
is a function that takes a string and returns a list of (a, String)
pairs. The Prelude provides
a type synonym for such functions:
type ReadS a = String -> [(a,String)]
Normally, a parser returns a singleton list, containing a value
of type a that was read from the input string and the remaining
string that follows what was parsed. If no parse was possible, however,
the result is the empty list, and if there is more than one possible
parse (an ambiguity), the resulting list contains more than one pair.
The standard function reads is a parser for any instance of Read:
reads :: (Read a) => ReadS a
We can use this function to define a parsing function for the string
representation of binary trees produced by showsTree. List comprehensions
give us a convenient idiom for constructing such parsers (An
even more elegant approach to parsing uses monads and parser
combinators. These are part of a standard parsing library distributed
with most Haskell systems.):
readsTree :: (Read a) => ReadS (Tree a)
readsTree ('<':s) = [(Branch l r, u) | (l, '|':t) <- readsTree s,
(r, '>':u) <- readsTree t ]
readsTree s = [(Leaf x, t) | (x,t) <- reads s]
Let's take a moment to examine this function definition in detail.
There are two main cases to consider: If the first character of the
string to be parsed is '<', we should have the representation of
a branch; otherwise, we have a leaf. In the first case, calling the
rest of the input string following the opening angle bracket s,
any possible parse must be a tree Branch l r with remaining string u,
subject to the following conditions:
The second defining equation above just says that to parse the representation of a leaf, we parse a representation of the element type of the tree and apply the constructor Leaf to the value thus obtained.
We'll accept on faith for the moment that there is a Read (and Show) instance of Int (among many other types), providing a reads that behaves as one would expect, e.g.:
(reads "5 golden rings") :: [(Int,String)] => [(5, " golden rings")]
With this understanding, the reader should verify the following evaluations:
| readsTree "<1|<2|3>>" | => | [(Branch (Leaf 1) (Branch (Leaf 2) (Leaf 3)), "")] |
| readsTree "<1|2" | => | [] |
There are a couple of shortcomings in our definition of readsTree.
One is that the parser is quite rigid, allowing no white space before
or between the elements of the tree representation; the other is that
the way we parse our punctuation symbols is quite different from the
way we parse leaf values and subtrees, this lack of uniformity making
the function definition harder to read. We can address both of these
problems by using the lexical analyzer provided by the Prelude:
lex :: ReadS String
lex normally returns a singleton list containing a
pair of strings: the first lexeme in the input string and the remainder
of the input. The lexical rules are those of Haskell programs,
including comments, which lex skips, along with whitespace.
If the input string is empty or contains only whitespace and comments,
lex returns [("","")]; if the input is not empty in this sense,
but also does not begin with a valid lexeme after any leading whitespace
and comments, lex returns [].
Using the lexical analyzer, our tree parser now looks like this:
readsTree :: (Read a) => ReadS (Tree a)
readsTree s = [(Branch l r, x) | ("<", t) <- lex s,
(l, u) <- readsTree t,
("|", v) <- lex u,
(r, w) <- readsTree v,
(">", x) <- lex w ]
++
[(Leaf x, t) | (x, t) <- reads s ]
We may now wish to use readsTree and showsTree to declare (Read a) => Tree a an instance of Read and (Show a) => Tree a an instance of Show. This would allow us to use the generic overloaded functions from the Prelude to parse and display trees. Moreover, we would automatically then be able to parse and display many other types containing trees as components, for example, [Tree Int]. As it turns out, readsTree and showsTree are of almost the right types to be Show and Read methods, needing only the addition of an extra parameter each that has do do with parenthesization of forms with infix constructors. We refer the interested reader to §D for details.
We can test the Read and Show instances by applying (read . show)
(which should be the identity) to some trees, where read is a
specialization of reads:
read :: (Read a) => String -> a
This function fails if there is not a unique parse or if the input
contains anything more than a representation of one value of type a
(and possibly, comments and whitespace).
Recall the Eq instance for trees we presented in Section
5; such a declaration is
simple---and boring---to produce: We require that the
element type in the leaves be an equality type; then, two leaves are
equal iff they contain equal elements, and two branches are equal iff
their left and right subtrees are equal, respectively. Any other two
trees are unequal:
instance (Eq a) => Eq (Tree a) where
(Leaf x) == (Leaf y) = x == y
(Branch l r) == (Branch l' r') = l == l' && r == r'
_ == _ = False
Fortunately, we don't need to go through this tedium every time we
need equality operators for a new type; the Eq instance can be
derived automatically from the data declaration if we so specify:
data Tree a = Leaf a | Branch (Tree a) (Tree a) deriving Eq
The deriving clause implicitly produces an Eq instance declaration
just like the one in Section 5. Instances of Ord,
Enum, Ix, Read, and Show can also be generated by the
deriving clause.
[More than one class name can be specified, in which case the list
of names must be parenthesized and the names separated by commas.]
The derived Ord instance for Tree is slightly more complicated than
the Eq instance:
instance (Ord a) => Ord (Tree a) where
(Leaf _) <= (Branch _) = True
(Leaf x) <= (Leaf y) = x <= y
(Branch _) <= (Leaf _) = False
(Branch l r) <= (Branch l' r') = l == l' && r <= r' || l <= l'
This specifies a lexicographic order: Constructors are ordered
by the order of their appearance in the data declaration, and the
arguments of a constructor are compared from left to right. Recall
that the built-in list type is semantically equivalent to an ordinary
two-constructor type. In fact, this is the full declaration:
data [a] = [] | a : [a] deriving (Eq, Ord) -- pseudo-code
(Lists also have a Text instance, which is not derived.)
The derived Eq and Ord instances for lists are the usual ones; in
particular, character strings, as lists of characters, are ordered as
determined by the underlying Char type, with an initial substring
comparing less than a longer string; for example, "cat" < "catalog".
In practice, Eq and Ord instances are almost always derived, rather than user-defined. In fact, we should provide our own definitions of equality and ordering predicates only with some trepidation, being careful to maintain the expected algebraic properties of equivalence relations and total orders. An intransitive (==) predicate, for example, could be disastrous, confusing readers of the program and confounding manual or automatic program transformations that rely on the (==) predicate's being an approximation to definitional equality. Nevertheless, it is sometimes necessary to provide Eq or Ord instances different from those that would be derived; probably the most important example is that of an abstract data type in which different concrete values may represent the same abstract value.
An enumerated type can have a derived Enum instance, and here again,
the ordering is that of the constructors in the data declaration.
For example:
data Day = Sunday | Monday | Tuesday | Wednesday
| Thursday | Friday | Saturday deriving (Enum)
Here are some simple examples using the derived instances for this type:
| [Wednesday..Friday] | => | [Wednesday, Thursday, Friday] |
| [Monday, Wednesday ..] | => | [Monday, Wednesday, Friday] |
Derived Read (Show) instances are possible for all types whose component types also have Read (Show) instances. (Read and Show instances for most of the standard types are provided by the Prelude. Some types, such as the function type (->), have a Show instance but not a corresponding Read.) The textual representation defined by a derived Show instance is consistent with the appearance of constant Haskell expressions of the type in question. For example, if we add Show and Read to the deriving clause for type Day, above, we obtain
show [Monday..Wednesday] => "[Monday,Tuesday,Wednesday]"
Monads are built on polymorphic types such as lists. The monad is defined by a set of instances in the monadic classes for this underlying polymorphic type.
Mathematically, monads are defined by set of laws which govern the monadic operations. Haskell includes other overloaded operations that are governed by laws, at least informally. For example, x /= y and not (x == y) ought to be the same. However, since both == and /= are class methods in the Eq class, there is no way to assure that == and =/ are related in this manner for arbitrary instances of Eq. In the same sense, the monadic laws presented here are not enforced by Haskell, but should be obeyed by all instances of a monadic class.
There are four classes associated with monads: Functor, Monad, MonadZero, and MonadPlus; none of them are derivable. In addition to IO, two other types in the Prelude are members of the monadic classes: lists ([]) and exceptions (Maybe). We will discuss only the instances for lists. The Maybe type behaves as a truncated list in monadic operations: Nothing is the same as [] and Just x is the same as [x].
The Functor class, already discussed in section 5, defines a single operation: map. The map function applies an operation to the objects inside a container (polymorphic types can be thought of as containers for values of another type), returning a container of the same shape. These laws apply to map in the class Functor:
| map id | = | id |
| map (f . g) | = | map f . map g |
These laws ensure that the container shape is unchanged by map and that the contents of the container are not re-arranged by the mapping operation.
The Monad class defines two basic operators: >>= (bind) and return.
class Monad m where
(>>=) :: m a -> (a -> m b) -> m b
(>>) :: m a -> m b -> m b
return :: a -> m a
m >> k = m >>= \_ -> k
The bind operations, >> and >>=, combine two monadic values while
the return operation injects a value into the monad (container).
The signature of >>=, Monad m => m a -> (a -> m b) -> m b, helps
us to understand this operation: ma >>= \v -> mb
combines a monadic value ma containing values
of type a and a function which operates
on a value v of type a returns the monadic value mb. The
result is to combine ma and mb into a
monadic value containing b. The >>
function is used when the function does not need the value produced by
the first monadic operator. The exact
meaning of binding depends of the particular monad being used. For
example, in the IO monad, x >>= y performs two actions sequentially,
passing the result of the first into the second. For lists, you can
think of the monadic functions
as dealing with multiple values. Monadic binding takes
a set (list) of values and applies a function to each of them,
collecting all generated values together. The return function
creates a singleton list.
Monadic list operations should already be familiar: list
comprehensions (as well as do expressions) are actually syntactic
sugar for monadic operators. In fact, in spite of their name, list
comprehensions can be used with arbitrary monads.
These following three expressions are all different syntax for the
same thing:
[(x,y) | x <- [1,2,3] , y <- [4,5,6]]
do x <- [1,2,3]
y <- [4,5,6]
return (x,y)
[1,2,3] >>= (\ x -> [4,5,6] >>= (\y -> return (x,y)))
The laws which govern >>= and return are:
| return a >>= k | = | k a |
| m >>= return | = | m |
| map f xs | = | xs >>= return . f |
| m >>= (\x -> k x >>= h)) | = | (m >>= k) >>= h |
The class MonadZero is used for monads that have a zero element:
class (Monad m) => MonadZero m where
zero :: m a
The zero element obeys the following laws:
| m >>= \x -> zero | = | zero |
| zero >>= m | = | zero |
For lists, the zero value is [], the empty list. The I/O monad has no zero element and is not a member of this class.
The class MonadPlus contains monads which have a plus
operation which combines the contents of two containers:
class (MonadZero m) => MonadPlus m where
(++) :: m a -> m a -> m a
Instances of MonadPlus should obey the following laws:
| m ++ zero | = | m |
| zero ++ m | = | m |
The ++ operator is ordinary list concatenation in the list monad.