Since Haskell is a functional language, one would expect functions to play a major role, and indeed they do. In this section, we look at several aspects of functions in Haskell.
First, consider this definition of a function which adds its two
arguments:
add :: Int -> Int -> Int
add x y = x + y
This is an example of a curried function. (The name
curry derives from the person who popularized the idea: Haskell
Curry. To get the effect of an uncurried function, we could use
a tuple, as in:
add (x,y) = x + y
But then we see that this version of add is really just a function
of one argument!) An application of add has the form add e1
e2, and is equivalent to (add e1) e2, since function
application associates to the left. In other words, applying
add to one argument yields a new function which is then applied to
the second argument. This is consistent with the type of add,
Int->Int->Int, which is equivalent to Int->(Int->Int); i.e. ->
associates to the right. Indeed, using add, we can define
inc in a different way from what we did earlier:
inc = add 1
This is an example of the partial application of a curried
function, and is one way that a function can be returned as a value.
Let's consider a case in which it's useful to pass a function as an
argument. The well-known map function is a perfect example:
map :: (a->b) -> [a] -> [b]
map f [] = []
map f (x:xs) = f x : map f xs
[Function application has higher precedence than any infix
operator, and thus the right-hand side of the second equation parses
as (f x) : (map f xs).] The map function is a polymorphic and
its type indicates clearly that its first argument is a function; note
also that the two a's must be instantiated with the same type
(likewise for the b's). As an example of the use of map, we can
increment the elements in a list:
map (add 1) [1,2,3] => [2,3,4]
These examples demonstrate the first-class nature of functions, which when used in this way are usually called higher-order functions.
Instead of using equations to define functions, we can also define
them "anonymously" via a lambda abstraction. For example, a
function equivalent to inc could be written as \x -> x+1.
Similarly, the function add is equivalent to \x -> \y -> x+y.
Nested lambda abstractions such as this may be written using the
equivalent shorthand notation \x y -> x+y. In fact, the equations:
inc x = x+1
add x y = x+y
are really shorthand for:
inc = \x -> x+1
add = \x y -> x+y
We will have more to say about such equivalences later.
In general, given that x has type t1 and exp has type t2, then \x->exp has type t1->t2.
Infix operators are really just functions, and can also be defined
using equations. For example, here is a definition of a
list concatenation operator:
(++) :: [a] -> [a] -> [a]
[] ++ ys = ys
(x:xs) ++ ys = x : (xs++ys)
[Lexically, infix operators consist entirely of "symbols," as
opposed to normal identifiers which are alphanumeric (§2.3).
Haskell has no prefix operators, with the exception of minus (-),
which is both infix and prefix.]
As another example, an important infix operator on functions is that
for function composition:
(.) :: (b->c) -> (a->b) -> (a->c)
f . g = \ x -> f (g x)
Since infix operators are really just functions, it makes sense to be able to partially apply them as well. In Haskell the partial application of an infix operator is called a section. For example:
| (x+) | = | \y -> x+y |
| (+y) | = | \x -> x+y |
| (+) | = | \x y -> x+y |
[The parentheses are mandatory.]
The last form of section given above essentially coerces an infix operator into an equivalent functional value, and is handy when passing an infix operator as an argument to a function, as in map (+) [1,2,3] (the reader should verify that this returns a list of functions!). It is also necessary when giving a function type signature, as in the examples of (++) and (.) given earlier.
We can now see that add defined earlier is just (+), and inc is
just (+1)! Indeed, these definitions would do just fine:
inc = (+ 1)
add = (+)
We can coerce an infix operator into a functional value, but can we go the other way? Yes---we simply enclose an identifier bound to a functional value in backquotes. For example, x `add` y is the same as add x y. (Note carefully that add is enclosed in backquotes, not apostrophes as used in the syntax of characters; i.e. 'f' is a character, whereas `f` is an infix operator. Fortunately, most ASCII terminals distinguish these much better than the typefont used in this manuscript.) Some functions read better this way. An example is the predefined list membership predicate elem; the expression x `elem` xs can be read intuitively as "x is an element of xs."
[There are some special rules regarding sections involving the prefix/infix operator - (§3.5,§3.4).]
At this point, the reader may be confused at having so many ways to define a function! The decision to provide these mechanisms partly reflects historical conventions, and partly reflects the desire for consistency (for example, in the treatment of infix vs. regular functions).
A fixity declaration can be given for any infix operator or
constructor (including those made from ordinary identifiers, such as
`elem`). (Fixity declarations must only appear at the very
beginning of a Haskell module, as will be described in Section
10.) This declaration specifies a precedence level from
0 to 9 (with 9 being the strongest; normal application is assumed to
have a precedence level of 10), and left-, right-, or
non-associativity. For example, the fixity declarations for ++ and
. are:
infixr 5 ++
infixr 9 .
Both of these specify right-associativity, the first with a precedence
level of 5, the other 9. Left associativity is specified via
infixl, and non-associativity by infix. Also, the fixity of more
than one operator may be specified with the same fixity declaration.
If no fixity declaration is given for a particular operator, it
defaults to infixl 9. (See §5.6 for a detailed definition
of the associativity rules.)
Suppose bot is defined by:
bot = bot
In other words, bot is a non-terminating expression. Abstractly, we
denote the value of a non-terminating expression as _|_ (read
"bottom"). Expressions that result in some kind of a run-time
error, such as 1/0, also have this value. Such an error is not
recoverable: programs will not continue past these errors. Errors
encountered by the I/O system, such as an end-of-file error, are
recoverable and are handled in a different manner. (Such an I/O error
is really not an error at all but rather an exception. Much more will
be said about exceptions in Section 7.)
A function f is said to be strict if, when applied to a
nonterminating expression, it also fails to terminate. In other
words, f is strict iff the value of f bot is _|_. For most
programming languages, all functions are strict. But this is
not so in Haskell. As a simple example, consider const1, the
constant 1 function, defined by:
const1 x = 1
The value of const1 bot in Haskell is 1. Operationally speaking,
since const1 does not "need" the value of its argument, it never
attempts to evaluate it, and thus never gets caught in a
nonterminating computation. For this reason, non-strict functions are
also called "lazy functions," and are said to evaluate their
arguments "lazily," or "by need."
Since error and nonterminating values are semantically the same in Haskell, the above argument also holds for errors. For example, const1 (1/0) also evaluates properly to 1.
Non-strict functions are extremely useful in a variety of contexts. The main advantage is that they free the programmer from many concerns about evaluation order. Computationally expensive values may be passed as arguments to functions without fear of them being computed if they are not needed. An important example of this is a possibly infinite data structure.
Another way of explaining non-strict functions is that Haskell
computes using definitions rather than the assignments found in
traditional languages. Read a declaration such as
v = 1/0
as `define v as 1/0' instead of `compute 1/0 and store the
result in v'. Only if the value (definition) of v is needed
will the division by zero error occur. By itself, this
declaration does not imply any computation. Assignments are ordered:
the meaning of assignments depends on the order in which they are
executed. However, definitions can be presented in any order without
changing their meaning.
One advantage of the non-strict nature of Haskell is that data constructors are non-strict, too. This should not be surprising, since constructors are really just a special kind of function (the distinguishing feature being that they can be used in pattern matching). For example, the constructor for lists, (:), is non-strict.
Non-strict constructors permit the definition of (conceptually)
infinite data structures. Here is an infinite list of ones:
ones = 1 : ones
Perhaps more interesting is the function numsFrom:
numsFrom n = n : numsFrom (n+1)
Thus numsFrom n is the infinite list of successive integers
beginning with n. From it we can construct an infinite list of
squares:
squares = map (^2) (numsfrom 0)
(Note the use of a section; ^ is the infix exponentiation operator.)
Of course, eventually we expect to extract some finite portion of the list for actual computation, and there are lots of predefined functions in Haskell that do this sort of thing: take, takeWhile, filter, and others. The definition of Haskell includes a large set of built-in functions and types -- this is called the "Standard Prelude". The complete Standard Prelude is included in Appendix A of the Haskell report; see the portion named PreludeList for many useful functions involving lists. For example, take removes the first n elements from a list:
take 5 squares => [0,1,4,9,16]
The definition of ones above is an example of a circular list. In most circumstances laziness has an important impact on efficiency, since an implementation can be expected to implement the list as a true circular structure, thus saving space.
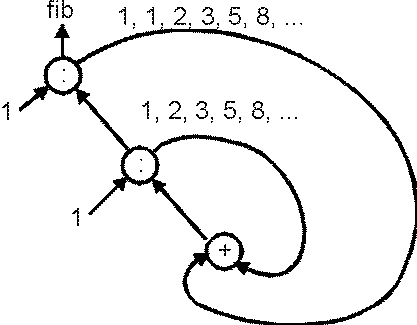
For another example of the use of circularity, the Fibonacci sequence
can be computed efficiently as the following infinite sequence:
fib = 1 : 1 : [ a+b | (a,b) <- zip fib (tail fib) ]
where zip is a Standard Prelude function that returns the pairwise
interleaving of its two list arguments:
zip (x:xs) (y:ys) = (x,y) : zip xs ys
zip xs ys = []
Note how fib, an infinite list, is defined in terms of itself, as if
it were "chasing its tail." Indeed, we can draw a picture of this
computation as shown in Figure 1.

For another application of infinite lists, see Section 4.4.
Haskell has a built-in function called error whose type is String->a. This is a somewhat odd function: From its type it looks as if it is returning a value of a polymorphic type about which it knows nothing, since it never receives a value of that type as an argument!
In fact, there is one value "shared" by all types: _|_.
Indeed, semantically that is exactly what value is always returned by
error (recall that all errors have value _|_). However, we can
expect that a reasonable implementation will print the string argument
to error for diagnostic purposes. Thus this function is useful when
we wish to terminate a program when something has "gone wrong." For
example, the actual definition of head taken from the Standard
Prelude is:
head (x:xs) = x
head [] = error "head{PreludeList}: head []"
The Gentle Introduction To Haskell
back next