
| 
| |
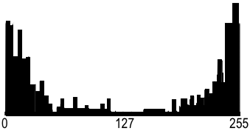
| Greyscale image "Boat" | Its grey level histogram | |

| 
| 
|
| Binary regions for T = 26 | Binary regions for T = 133 | Binary regions for T = 235 |

| 
| 
|
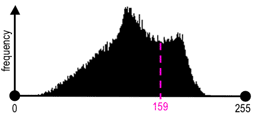
| Greyscale image "Baboon" | Its grey level histogram | Binary regions for T = 159 |
Segmentation partitions an image into distinct regions containing each pixels with similar attributes. To be meaningful and useful for image analysis and interpretation, the regions should strongly relate to depicted objects or features of interest. Meaningful segmentation is the first step from low-level image processing transforming a greyscale or colour image into one or more other images to high-level image description in terms of features, objects, and scenes. The success of image analysis depends on reliability of segmentation, but an accurate partitioning of an image is generally a very challenging problem.
Segmentation techniques are either contextual or non-contextual. The latter take no account of spatial relationships between features in an image and group pixels together on the basis of some global attribute, e.g. grey level or colour. Contextual techniques additionally exploit these relationships, e.g. group together pixels with similar grey levels and close spatial locations.
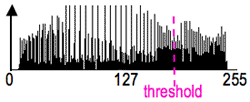
Thresholding is the simplest non-contextual segmentation technique. With a single threshold, it transforms a greyscale or colour image into a binary image considered as a binary region map. The binary map contains two possibly disjoint regions, one of them containing pixels with input data values smaller than a threshold and another relating to the input values that are at or above the threshold. The former and latter regions are usually labelled with zero (0) and non-zero (1) labels, respectively. The segmentation depends on image property being thresholded and on how the threshold is chosen.
Generally, the non-contextual thresholding may involve two or more thresholds as well as produce more than two types of regions such that ranges of input image signals related to each region type are separated with thresholds. The question of thresholding is how to automatically determine the threshold value.
The most common image property to threshold is pixel grey level: g(x,y) = 0 if
f(x,y) < T and g(x,y) = 1 if f(x,y) ≥ T,
where T is the threshold. Using
two thresholds, T1 < T1, a range of grey levels
related to region 1 can be defined: g(x,y) = 0 if
f(x,y) < T1 OR f(x,y) > T2
and g(x,y) = 1 if T1 ≤ f(x,y) ≤ T2.

| 
| |
| Greyscale image "Boat" | Its grey level histogram | |

| 
| 
|
| Binary regions for T = 26 | Binary regions for T = 133 | Binary regions for T = 235 |

| 
| 
|
| Greyscale image "Baboon" | Its grey level histogram | Binary regions for T = 159 |
The main problems are whether it is possible and, if yes, how to choose an adequate threshold or a number of thresholds to separate one or more desired objects from their background. In many practical cases the simple thresholding is unable to segment objects of interest, as shown in the above images.
A general approach to thresholding
is based on assumption that images are multimodal, that is, different objects
of interest relate to distinct peaks (or modes) of the 1D signal histogram. The thresholds
have to optimally separate these peaks in spite of typical overlaps between the
signal ranges corresponding to individual peaks. A threshold in the valley
between two overlapping peaks separates their main bodies but inevitably detects or
rejects falsely some pixels with intermediate signals. The optimal threshold that minimises
the expected numbers of false detections and rejections may not coincide with the
lowest point in the valley between two overlapping peaks:
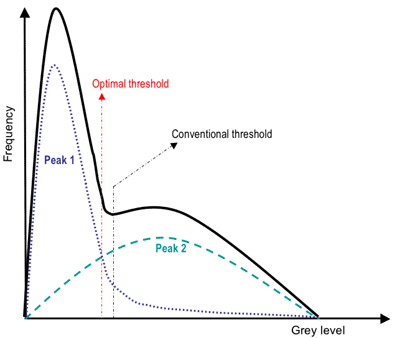
Since the threshold separates the background from the object, the adaptive separation may take account of empirical probability distributions of object (e.g. dark) and background (bright) pixels. Such a threshold has to equalise two kinds of expected errors: of assigning a background pixel to the object and of assigning an object pixel to the background. More complex adaptive thresholding techniques use a spatially varying threshold to compensate for local spatial context effects (such a spatially varying threshold can be thought as a background normalisation).
A simple iterative adaptation of the threshold is based on
successive refinement of the estimated peak positions. It assumes that
(i) each peak coincides with the mean grey level for all pixels
that relate to that peak and (ii)
the pixel probability decreases monotonically on
the absolute difference between the
pixel and peak values both for an object and background peak.
The classification of the object and background pixels is
done at each iteration j by using the threshold Tj found
at previous iteration. Thus, at iteration j, each grey level f(x,y)
is assigned first to the object or background class (region)
if f(x,y) ≤ Tj
or f(x,y) > Tj, respectively. Then, the new threshold,
Tj+1 = 0.5(μj,ob + μj,bg)
where μj,ob and μj,bg
denote the mean grey level at
iteration j for the found object and background pixels, respectively:

Color segmentation may be more accurate because of more information at the pixel level
comparing to greyscale images. The standard Red-Green-Blue (RGB) colour representation has
strongly interrelated colour components, and a number of other colour systems (e.g. HSI
Hue-Saturation-Intensity) have been designed in order to exclude redundancy, determine actual
object / background colours irrespectively of illumination, and obtain more
more stable segmentation. An example below (from
http://www.matrix-vision.com/products/software)
shows that colour thresholding can focus on an object of interest
much better than its greyscale analogue:

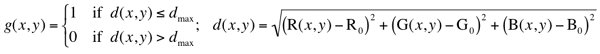
Also, there can be an ellipsoidal decision surface if independent distance
thresholds are specified for the R, G, and B components. Generally, colour segmentation, just as
the greyscale one,
may be based on the analysis of 3D colour histograms or their more convenient 2D
projections. A colour histogram is built by partitioning of the colour space onto a
fixed number of bins such that the colours within each bin are considered as the
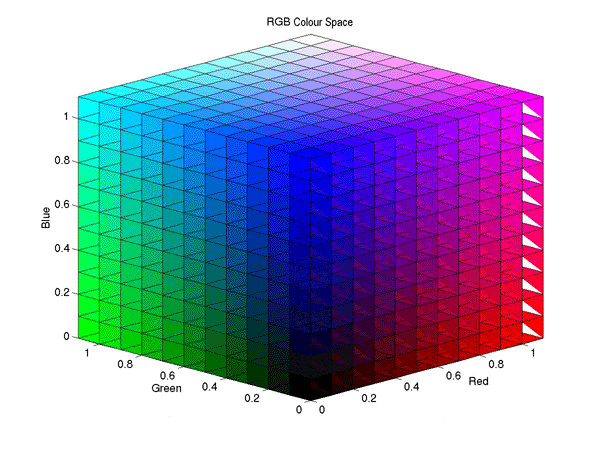
same colour. An example below of the partitioned 11×11×11
RGB colour space is from
(http://www.owlnet.rice.edu/~elec301/Projects02/artSpy/color.html):

| 
|
| Colour image "Baboon" | Its colour 6×6×6 histogram (sphere-size-coded bin values) |

| 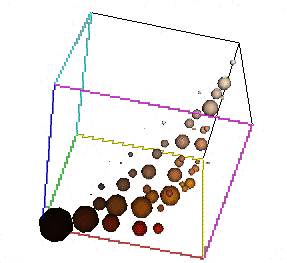
|
| Colour image "Clown" | Its colour 6×6×6 histogram (sphere-size-coded bin values) |
If a chosen colour space separates colourless intensity values from
intensity-independent colour components (such as hue and saturation or normalised
red / blue colurs),
colour segmentation can be based on a few pre-selected colours, e.g. on the eight primary
colours (black, red, green, blue, yellow, cyan, magenta, white). An example below shows
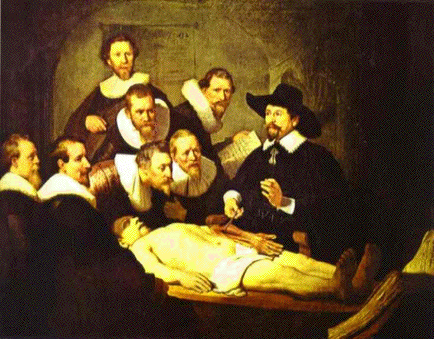
a digitised picture of the Rembrandt's canvas
"Doctor Nicolaes Tulp's Demonstration of the Anatomy of the Arm" (1632;
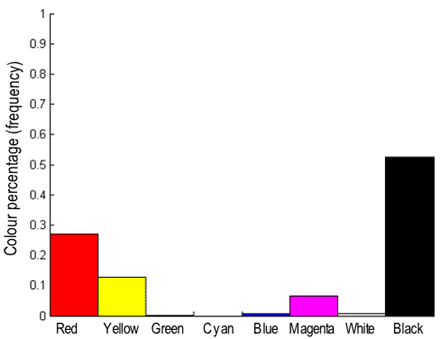
Mauritshuis Museum, The Hague, The Netherlands), its 8-bin histogram of the primary colours, and
the corresponding colour regions:
| 
| 
|
| Digitised Rembrandt's canvas | Colour 8-bin histogram | Regions of the primary colours |
| (www.abcgallery.com/R/rembrandt/) | (http://rsb.info.nih.gov/ij/plugins/color-inspector.html) | |
More efficient adaptive thresholding of greyscale images can be extended to colour images, too, by replacing mean grey levels for each colour region with its mean colors, e.g. RGB-vectors with the mean component values.
Non-contextual thresholding groups pixels with no account of their relative locations in the image plane. Contextual segmentation can be more successful in separating individual objects because it accounts for closeness of pixels that belong to an individual object. Two basic approaches to contextual segmentation are based on signal discontinuity or similarity. Discontinuity-based techniques attempt to find complete boundaries enclosing relatively uniform regions assuming abrupt signal changes across each boundary. Similarity-based techniques attempt to directly create these uniform regions by grouping together connected pixels that satisfy certain similarity criteria. Both the approaches mirror each other, in the sense that a complete boundary splits one region into two.
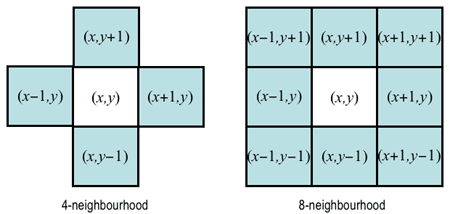
Pixel connectivity is defined in terms of pixel neighbourhoods. A normal
rectangular sampling pattern producing a finite arithmetic lattice {(x,y):
x = 0, 1, ..., X−1; y = 0, 1, ..., Y−1}
supporting digital images allows us to define two types of neighbourhood surrounding
a pixel. A 4-neighbourhood {(x−1,y), (x,y+1),
(x+1,y), (x,y−1)} contains only the pixels above, below,
to the left and to the right of the central pixel (x,y). An 8-neighbourhood
adds to the 4-neighbourhood four diagonal neighbours:
{(x−1,y−1),(x−1,y), (x−1,y+1),
(x,y+1), (x+1,y+1), (x+1,y),
(x+1,y−1), (x,y−1)}.
A 4-connected path from a pixel p1 to another pixel pn is defined as the sequence of pixels {p1, p2, ..., pn} such that pi+1 is a 4-neighbour of pi for all i = 1, ..., n−1. The path is 8-connected if pi+1 is an 8-neighbour of pi. A set of pixels is a 4-connected region if there exists at least one 4-connected path between any pair of pixels from that set. The 8-connected region has at least one 8-connected path between any pair of pixels from that set.
One of the simplest and most common algorithms for labelling connected regions after
greyscale or colour thresholding exploits the "grassfire" or "wave
propagation" principle: after
a "fire" or "wave" starts at one pixel, it propagates to any of
the pixel's 4- or 8-neighbours detected by thresholding. Each already visited (i.e.
"burnt away" or "wet") pixel cannot be visited
again, and after the entire connected region is labelled, its
pixels are assigned a region number, and the procedure continues to search for
the next connected region. Magenta and yellow stars below indicate the fire, or wave
front and the burnt
away pixels, respectively. To label a region, the fire starts from its first
chosen pixel:
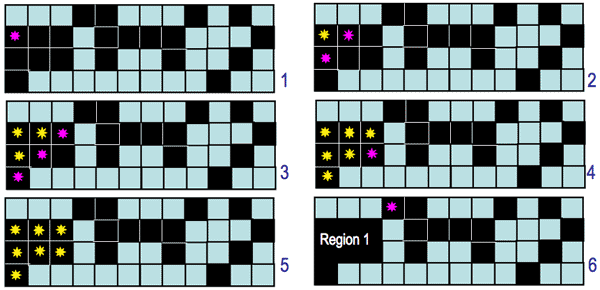
The 4- and 8-connectivity produce different segmentation results:
Moreover,
each definition leads to contradictions between the discrete and continuous
cases. For example, an one-pixel-wide vertical or horizontal 8-connected line separates two
8-connected regions but this separation does not hold after the line is only
slightly rotated with respect to the image lattice:
|

|
At the same time, the like 4-connected
line breaks into disjoint pieces after such a rotation:

|
|
Modern digital geometry
has developed theoretically justified approaches to escape these problems. In many
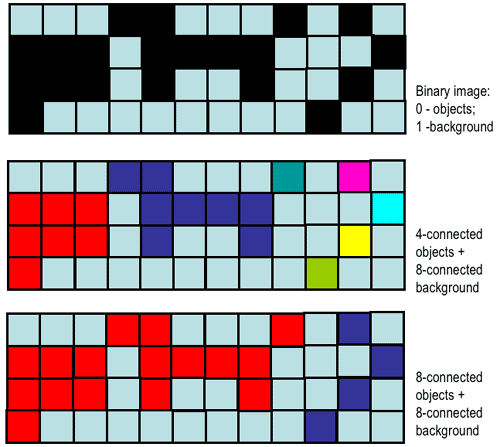
practical cases, the connectivity is simply defined variously for objects (foreground
pixels) and background, e.g. 4-connectivity for objects and 8-connectivity for background
or vice versa:

| 
| 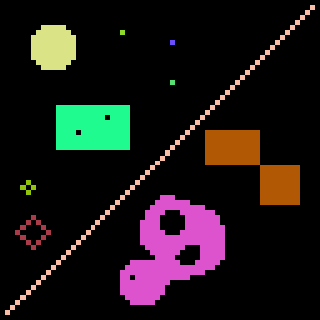
|
| Binary image 64×64 (zoom by a factor of 5) | 86 foreground 4-connected regions | 10 foreground 8-connected regions |
| (http://www.dca.fee.unicamp.br/projects/khoros/mmach/tutor/toolbox/basicl/labeling/front-page.html) | ||
The uniformity or non-uniformity of pixels to form a connected region is represented by a uniformity predicate, i.e. a logical statement, or condition being true if pixels in the regions are similar with respect to some property (colour, grey level, edge strength, etc). A common predicate restricts signal variations over a neighbourhood: the predicate P(R), where R denotes a connected region, is TRUE if |f(x,y) − f(x+ξ,y+η)| ≤ Δ and FALSE otherwise (here, (x,y) and (x+ξ,y+η) are the coordinates of neighbouring pixels in region R. This predicate does not restrict the grey level variation within a region because small changes in signal values can accumulate over the region.
Intra-region signal variations can be restricted with a similar predicate: P(R) = TRUE if |f(x,y) − &muR| ≤ &Delta and FALSE otherwise where (x,y) is a pixel from the region R and μR is the mean value of signals f(x,y) over the entire region R.
The bottom-up region growing algorithm
starts from a set of seed pixels defined by the user and sequentially adds a pixel to
a region provided that the pixel has not been assigned to any other region,
is a neighbour of that region,
and its addition preserves uniformity of the growing region.
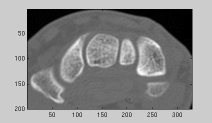
| 
| 
|
| Greyscale image | Seed regions | Region growing results |
| (http://www.lems.brown.edu/~msj/cs292/assign5/segment.html) | ||
Such a segmentation
is simple but unstable. It is very sensitive to a chosen uniformity predicate, i.e. small
changes of the uniformity threshold may result in large changes of the regions found.
Also, very different segmentation maps are obtained under different
routes of scanning an image, different modes of exhausting neighbours of each region,
different seeds, and different types of pixel connectivity.
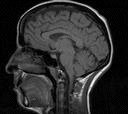
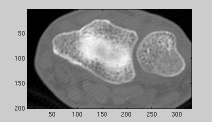
| 
| 
|
| Greyscale image (zoom by a factor of 2) | 4-connected region growing | 8-connected region growing |
| (http://www.comp.leeds.ac.uk/ai21/examples/images/rgrow.html) | ||
| 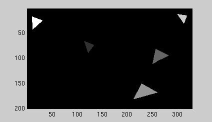
| 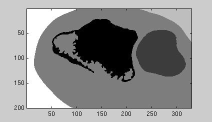
|
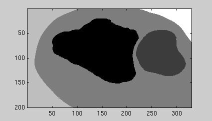
| Greyscale image | Seed regions: variant 1 | Region growing results |
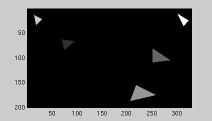
| 
| |
| Seed regions: variant 2 | Region growing results | |
| (http://www.lems.brown.edu/~msj/cs292/assign5/segment.html) | ||
Generally, a "good" complete segmentation must satisfy the following criteria:
Region growing satisfies the 3rd and 4th criteria, but not the others. The first two criteria are not satisfied because, in general, the number of seeds may not be sufficient to create a region for every pixel. The 5th criterion may not hold because the regions grown from two nearby seeds are always regarded as distinct, even if those seeds are defined within a potentially uniform part of the image.
The top-down split-and-merge algorithm considers initially the entire image to be a single region and then iteratively splits each region into subregions or merges adjacent regions until all regions become uniform or until the desired number of regions have been established.
A common splitting strategy for a square image is to divide it recursively into
smaller and smaller quadrants until, for any region R, the uniformity predicate
P(R) is TRUE. The strategy builds a top-down quadtree: if P(image)
is FALSE, the image is divided into four quadrants; if P(quadrant) is FALSE, the
quadrant is divided into subquadrants; and so on:
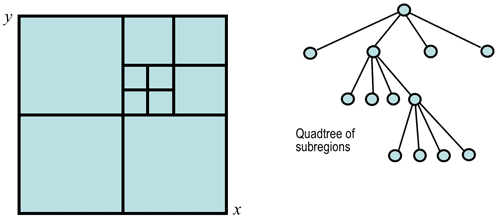
Grey level or colour pixel values by themselves are not sufficient for segmenting
natural highly-textured images like those shown below:

| 
| 
|
| Textured collage | Grey-level histogram | Segmentation by thresholding |

| 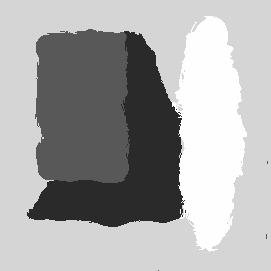
|
| Textured collage | Segmentation using local features |
| (http://www.sztaki.hu/~sziranyi/textu-iu.html) | |

| |
| Textured collage, actual region map, and segmentation using local features | |
| (http://www.ercim.org/publication/Ercim_News/enw64/mikes.html | |
Texture is a spatial property that characterises groups of pixels. A local measure of
texture is therefore computed over a neighbourhood. An example of the simplest statistical
measure is the variance of grey levels in a square n×n neighbourhood
centred on a pixel:
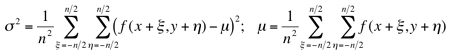

| 
|
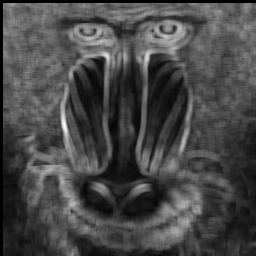
| Greyscale image "Baboon" | Variance image (7×7 window) |
| 
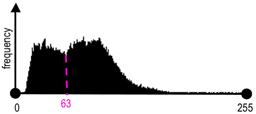
|
| Histogram of the variance image | Variance thresholding: T=63 |
For most of natural textures, simple statistical measures are of little use. If two textures of interest are periodic, they might be separated in the frequency domain by comparing the spectra of small samples taken from the two patterns. Spectral segmentation techniques typically use the radially or angularly integrated power spectrum of a region in an image. Radial integration sums power values within a ring of radius r and width Δr. Angular integration sums power values within a sector defined by a radius, r, an orientation, θ, and an angular width, Δθ. The ring-based measurement relates to the texture scale: a concentration of power at small or large radii signifies coarse or fine texture, respectively. The sector-based measurement relates to texture orientation: a texture oriented in a direction φ results in high power for a sector at angle θ = φ + π/2.
These lecture notes follow Chapter 10 "Segmentation" of the textbook