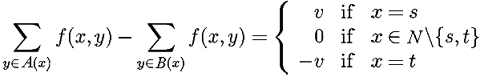
The search for a whole continuous 3-D surface making the minimum dissimilarity or maximum similarity between corresponding points of a stereo pair can be considered as combinatorial optimisation on graphs. The graphs describe binary relationships between the neighbouring disparities and signals that restrict the solution. Typically, the graph specifies neighborhoods, i.e. subsets of mutually dependent pixels or points, and weights of its nodes and edges characterize possible image signals and/or disparities. The surfaces are evaluated in terms of local and global energies accumulating the weights of nodes and edges. Generally, under dense 2D neighborhoods, an optimal minimum-energy solution is an NP-complete problem. But it can be at least approximately solved or sometimes is reduced to an exactly solvable particular case.
Let G = [N;E] denote a directed (linear) graph with a collection of nodes (vertices, points) N = {xa, xb, xc, …} and a subset E ⊆ N × N of ordered pairs (edges, arcs) (xα,xβ) of elements from N. A chain is a sequence of nodes x1, x2, … such that (xi, xi+1) ∈ E. A path is a sequence x1, x2, … such that (xi, xi+1) ∈ E or (xi+1, xi) ∈ E. Let A(x) = {y | y ∈ N; (x,y) ∈ E} and B(x) = {y | y ∈ N; (y,x) ∈ E} be subsets of the nodes after x and before x, respectively.
A network is a graph with two special nodes s and t called source and sink, respectively, and with a non-negative capacity c(x,y) ≥ 0 assigned to every edge (x,y) ∈ E. The function c: E → R≥0, where R≥0 is the set of non-negative real numbers, is called the capacity function.
A static flow of value v from s to t in a network G = [N;E] with a capacity function c is a function f: E → R≥0 that satisfies the linear constraints:
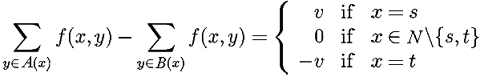
 .
.
The static maximum flow problem is to maximize the variable v subject to the above flow constraints. To simplify the notation, let (X,Y)); X ⊂ N, Y ⊂ N denote a set of all edges from nodes x ∈ X to nodes y ∈ Y. For any function g: E → R, let g(X,Y) denote the sum of values of the function over the set of edges:
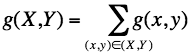
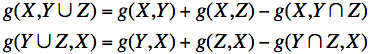
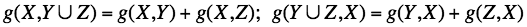
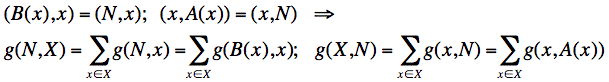
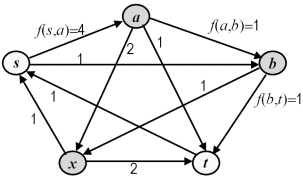
A cut C in G = [N;E] separating the source s and the sink t is a set of edges (X,N\X) such that s ∈ X and t ∈ N\X. The capacity of a cut (X,N\X) is c(X,N\X). A simple example below
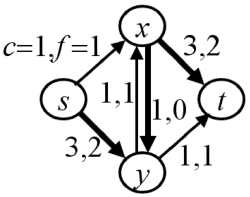
Lemma 1 [Ford, Fulkerson;1956]: Let f be a flow from s to t in a network [N; E], and let f have value v. If (X, N\X) is a cut, separating s and t, then
Proof: Since f is a flow, then f(s,N) − f(N,s) = v; f(x,N) − f(N,x) = 0 for all x ∈ N\{s,t}, and f(t,N) − f(N,t) = −v. Let us sum these equations over x ∈ X. Since s ∈ X and t ∈ N\X, the result is
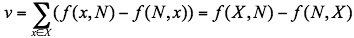
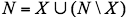 the above equality yields
the above equality yields
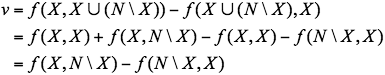
The equality in Lemma 1 states that the value of a flow from s to
t is equal to the net flow across any cut separating s and t.
The fundamental result concerning the maximal network flow is given by
MAX-FLOW MIN-CUT Theorem
[Ford, Fulkerson; 1956]: For any network the maximum flow value from
s to t is equal to the minimal cut capacity of all cuts
separating s and t.
Return to the local table of contents
Return to the global table of contents
Let a flow augmenting path with respect to a flow f be
defined as a path from s to t such that f < c on
forward edges of the path and f > 0 on reverse edges of the
path. The following corollary
is of fundamental importance in
searching for the maximal network flows:
Corollary 1 [Ford, Fulkerson; 1956]:
A flow f is maximal if and only if there is no flow
augmenting path with respect to f.
This corollary
states that in order to increase the value of a flow, it is
sufficient to search for improvements of a very restricted kind.
Let an edge (x,y) be called saturated with respect to a flow
f if f(x,y) = c(x,y) and called
flowless with respect
to f if f(x,y) = 0. An edge being both saturated and
flowless has zero capacity. A minimal cut is characterized in
terms of these notions by
Corollary 2 [Ford, Fulkerson; 1956]:
A cut (X, N\X) is minimal if
and only if every maximal flow saturates all edges of
(X, N\X) whereas all edges
of (N\X, X) are flowless
with respect to f.
Ford-Fulkerson labelling algorithm: Under mild restrictions on the capacity function, the proof of the max-flow min-cut theorem provides an algorithm for constructing a maximal flow and minimal cut in a network. To ensure termination, all the capacities should have integer values. Initialization is with the zero flow. Then a sequence of "labelings" is performed (Routine A below). Each labeling either results in a flow of higher value (Routine B below) or terminates with the conclusion that the present flow is maximal. Given an integral flow f, labels are assigned to nodes of the network according to Routine A. A node can be in one of three states: unlabeled(UL), labeled and scanned (LS), or labeled and unscanned (LUS). Each label has one of the forms (x+,ε) or (x−,ε) where x ∈ N and ε is a positive integer or ∞. Initially all nodes are UL.
Routine A: labeling
The labeling process searches systematically for a flow augmenting path from s to t (see Corollary 1). Information about the paths is carried along in the labels, so that if the sink is labelled, the resulting flow change along the path is readily made. On the other hand, if Routine A ends and the sink is not labelled, the flow is maximal and the set of edges leading from labelled (LUS,LS) nodes to unlabelled (UL) nodes is a minimal cut.
The labelling process is computationally efficient because once a node is labelled and scanned, it is ignored for the remainder of the process. Labelling a node x locates a path from s to x that can be the initial segment of a flow augmenting path. There may be many such paths from s to x, but it is sufficient to find one.
Computational complexity: Both the initial Ford-Fulkerson max-flow min-cut algorithm and the subsequent solutions of the same problem have polynomial time complexity (below, n = |N| is the size, or cardinality of the set of nodes N and m = |E| is the size of the set of edges E):
| Algorithm | Principle | Complexity |
|---|---|---|
| Ford--Fulkerson, 1956 | Finding flow augmenting paths | O(nm2) |
| Dinic, 1970 | Shortest augmenting paths in one step | O(n2m) |
| in a dense graph: | O(n3) | |
| in a sparse graph: | O(nm log(n)) | |
| Goldberg--Tarjan, 1985 | Pushing a pre-flow | O(nm log(n2/m)) |
Time complexity of the Ford-Fulkerson algorithm depends on how the flow augmenting paths are determined. The O(nm2) Edmonds-Karp algorithm implements the Ford-Fulkerson scheme by using the breadth-first search for the augmenting path being a shortest path from s to t in the residual graph (network) where each edge has unit length, or weight. For a given network G = [N; E] and a flow f, the residual network Gf induced by f consists of edges, Ef, that allow for increasing the flow. The additional flow permitted by the edge capacity is called the residual capacity of the edge:
Return to the local table of contents
Return to the global table of contents
Search strategies based on flow augmenting paths keep a flow at each step although the maximal flow is needed only at the very end. This is why these strategies turned to be less efficient than the subsequent ones based on a pre-flow notion coined by A. V. Karzanov in 1974. The Karzanov's pre-flow violates the flow conditions in that the in-flow and out-flow nodes may not be equal, the difference at node x being called the excess at x). If f is a pre-flow in a graph G = [N; E], then the excess e(x) at x is:
| f(x,y) ← f(x,y) + Δ | f(y,x) ← f(y,x) − Δ |
| e(x) ← e(x) − Δ | e(y) ← e(y) + Δ |
Return to the local table of contents
Return to the global table of contents
Greig et al. (see References) were the first who have shown how thew Bayesian denoising (restoration) of binary images can be reformulated as a minimum cut problem in a certain network and solved exactly with the max-flow/min-cut technique such as the aforementioned Ford-Fulkerson algorithm. Let x = (x1, …, xn) and y = (y1, …, yn) be a hidden noiseless and a measured noisy image, respectively, such that the measurements yi; i = 1,…,n, are conditionally independent given a noiseless image x. Each measured signal yi has a known conditional probability density function p(yi|xi), depending on x only through xi. Therefore,
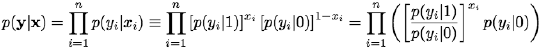
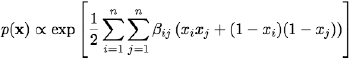
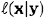 is as
follows:
is as
follows:
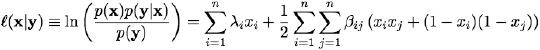
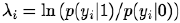 is a log-likelihood
ratio at pixel i. The Bayesian MAP estimate of the image maximises
the posterior likelihood:
is a log-likelihood
ratio at pixel i. The Bayesian MAP estimate of the image maximises
the posterior likelihood:
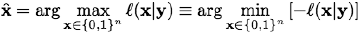
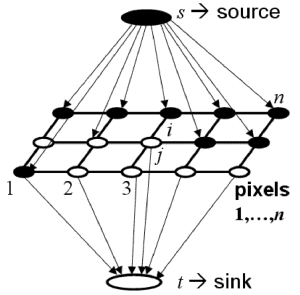
A capacitated network model for this optimisation problem contains n + 2 nodes, being a source s, a sink t, and the n pixels. If the log-likelihood ratio is positive λi > 0, there is a directed edge (s,i) from s to pixel i with capacity c(s,i) = λi; otherwise, there is a directed edge (i,t) from i to t with capacity c(i,t) = −λi. There is an undirected edge (i,j) between two pixels i and j with capacity c(i,j) = βij if these pixels are neighbours. Figure below exemplifies such a network model for restoring a binary image under a Markov-Gibbs prior model with the 4-neighbourhood interactions between pixels (here, signals y1,…,yn of an observed noisy image that result in positive, λi > 0, and non-positive, λi ≤ 0, log-likelihood ratios are shown by the black and white pixel nodes, respectively):
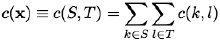
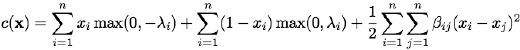
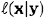 by a term
which does not depend
on x. Therefore, maximizing
by a term
which does not depend
on x. Therefore, maximizing 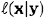 is equivalent
to finding the minimum cut of the above network: in the MAP estimate pixels
xi = 1 if they
are on the source side S of the minimum cut and xi = 0 otherwise.
Experiments conducted by Greig et al. (see References) have underscored the
importance of an adequate prior distribution because its global properties
very rapidly begin to dominate the likelihood contribution to the
posterior distribution. At the same time, the stochastic
optimization such as simulated annealing applied with a practicable
"cooling" schedule does
not necessarily yield a good approximation to the MAP estimate. According to the
"annealing theorem" of S. Geman and D. Geman,
the inverse logarithmic decrease with time of the temperature term in
a Gibbs distribution that controls the
annealing process guarantees that the MAP solution
will be eventually reached, but unfortunately this may take the infinite time.
is equivalent
to finding the minimum cut of the above network: in the MAP estimate pixels
xi = 1 if they
are on the source side S of the minimum cut and xi = 0 otherwise.
Experiments conducted by Greig et al. (see References) have underscored the
importance of an adequate prior distribution because its global properties
very rapidly begin to dominate the likelihood contribution to the
posterior distribution. At the same time, the stochastic
optimization such as simulated annealing applied with a practicable
"cooling" schedule does
not necessarily yield a good approximation to the MAP estimate. According to the
"annealing theorem" of S. Geman and D. Geman,
the inverse logarithmic decrease with time of the temperature term in
a Gibbs distribution that controls the
annealing process guarantees that the MAP solution
will be eventually reached, but unfortunately this may take the infinite time.
Accelerated solution: A ten-fold acceleration of the basic Ford-Falkerson algorithm is obtained for this network model by partitioning the input image into 2K×2K connected sub-images. The MAP estimate is calculated for each sub-image separately, then the sub-images are amalgamated to form a set of 2K−1×2K−1 larger sub-images. The MAP estimate is formed for each of them, and this process is continued until the MAP estimate of the complete image.
Return to the local table of contents
Return to the global table of contents
Theorem FD[Friedman, Drineas; 2005] (generally, it is considered as a part of combinatorial optimization folklore): Let xi ∈ {0,1}; i = 1,…,n, and let
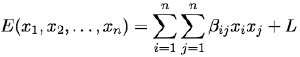
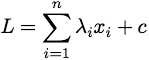 .
.
Proof: To prove the "if" direction, the energy can be rewritten as
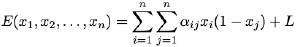
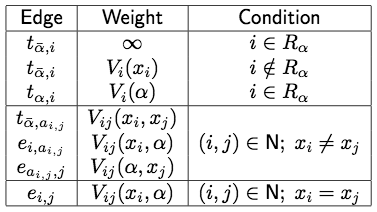
For altered linear terms Λ = γixi + σ there is an edge (s,i) with the weight wsi = γi if γi ≥ 0 and an edge (i,t) with wit = |γi| if γi < 0, so that all weights are non-negative.
The proof of "only if" is only slightly more complicated.
The MAP estimates based on the Markov-Gibbs posteriors with pairwise interactions result in the class of energy functions:
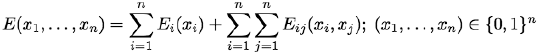
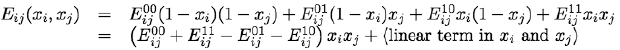
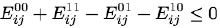
More sophisticated sufficient conditions for energy minimization using the min-cut techniques exist also for energy functions with k-wise pixel interaction, k > 2. But natural generalisations of the minimum cut problem to the case of more than two terminals, such as a multiway cut and minimum k-cut, are NP-hard apart from a few special cases with very restrictive conditions on energy functions:
The problem of finding a minimum weight multiway cut is NP-hard for any fixed k ≥ 3 (the case k = 2 is the minimum s-t cut problem). The minimum k-cut problem has polynomial time complexity for fixed k and is NP-hard if k is one of input variables. Both the problems have approximation algorithms that guarantee the solution within factor 2−2/k from the exact optimum.
When the energy functions involve multiple labels per pixel, the pixel-wise stochastic global minimization with simulated annealing (SA) or the deterministic pixel-wise local minimization with the ``greedy" iterated conditional modes (ICM) algorithm typically produce very poor results. Even in the simplest case of binary labeling considered above, the simulated annealing and ICM algorithms converge to stable points such that are too far from the global minimum. Although simulated annealing provably converges to the global minimum of energy, this could be obtained only in exponential time; this is why no practical implementation can closely approach the goal.
The main drawback of the simulated annealing or ICM algorithms is that they are pixel-wise, i.e. each iteration changes only one label in a single pixel in accord with the neighbouring labels. Therefore each iteration results in an extremely small move in the space of possible labellings. Obviously, the convergence rate should become faster under larger moves that simultaneously change labels in a large number of pixels.
Return to the local table of contents
Return to the global table of contents
As was already mentioned, the minimum multiway cut problem of finding the minimum capacity set of edges whose removal separates a given set of k terminals is NP-hard. But it has a provably good approximate solution that can be obtained with the exact min-cut / max-flow techniques. Let an isolating cut for a terminal si in a given set S = {s1,…,sk} be defined as a subset of edges whose removal separates si from the rest of the terminals. Then the following algorithm gives an approximate solution to the multicut problem:
Step 1 exploits k separate max-flow / min-cut computations. Because the removal of C from the graph disconnects every pair of terminals, it is a multiway cut.
Theorem [Vazirani, 2003]: Algorithm AMC guarantees a solution within a factor 2 − 2/k of the optimal solution.
Proof: Let Copt be an optimal multiway cut in a graph G = [N; E]. Then Copt can be considered as the union of k cuts as follows:
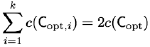
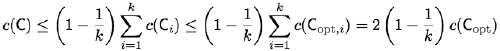
The minimum k-cut problem of finding a minimum-capacity set of edges whose removal leaves k connected components in a graph G has a natural factor 2 −2/k approximate solution:
Return to the local table of contents
Return to the global table of contents
Two fast approximate algorithms for energy minimization developed by Boykov, Veksler, and Zabih (see References) improve the poor convergence of simulated annealing by replacing pixel-wise changes with specific large moves. The resulting process converges to a solution that is provably within a known factor of the global energy minimum.
The energy function to be minimized is
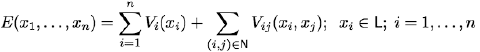
The approximate Boykov-Veksler-Zabih minimization algorithms work with any semimetric or metric Vij by using large α-β-swap or α-expansion moves respectively. The conditionally optimal moves are found with a min-cut / max-flow technique.
The α-β-swap for an arbitrary pair of labels α,β∈L is a move from a partition P for a current labelling x to a new partition P′ for a new labelling x′ such that Rλ = R′λ for any label λ ≠ α, β. In other words, this move changes only the labels α and β in their current region Rαβ = Rα ∪ Rβ whereas all other labels in R\Rαβ remain fixed. In the general case, after an α-β-swap some pixels change their labels from α to β and some others -- from β to α. A special variant is when the label α is assigned to some pixels previously labelled β.
The α-expansion of an arbitrary label α is a move from a partition P for a current labelling x to a new partition P′ for a new labelling x′ such that Rα ⊂ R′α and R\R′α = ∪λ∈L; λ ≠ αR′λ ⊂ R\Rα = ∪λ∈L; λ ≠ αRλ. In other words, after this move any subset of pixels can change their labels to α.
Energy minimization algorithms: The SA and ICM algorithms use standard pixel-wise relaxation moves changing one label each time. Such a move is both α-β-swap and α-expansion, so that these latter generalize the standard relaxation scheme. The algorithms based on these generalizations are sketched below.
Swap algorithm for semimetric interaction potentials
An iteration at Step 2 performs L individual α-expansion moves in the expansion algorithm and L2 individual α-β-swap moves in the swap algorithm. It is possible to prove that the minimisation terminates in a finite number of iterations being of order of the image size n. Actually, image segmentation and stereo reconstruction experiments conducted by Boykov, Kolmogorov, Veksler, and Zabih (see References) have shown that these algorithms converge to the local energy minimum just in a few iterations.
Given a current labelling x (partition P) and a pair
of labels (α,β) or a label α, the swap or expansion
moves, respectively, at Step 2.1 in the above algorithms
use the min-cut / max-flow
optimization techique to find a better labelling
![]() . This labelling
minimises the energy over all labellings within one α-β-swap
(the swap algorithm) or one α-expansion (the expansion
algorithm) of x and corresponds to a minimum cut of a specific
graph having O(n) nodes associated with pixels. The swap and
expansion graphs are different, and the
exact number of their pixels, their topology, and edge weights
vary from step to step in accord with the current partition.
. This labelling
minimises the energy over all labellings within one α-β-swap
(the swap algorithm) or one α-expansion (the expansion
algorithm) of x and corresponds to a minimum cut of a specific
graph having O(n) nodes associated with pixels. The swap and
expansion graphs are different, and the
exact number of their pixels, their topology, and edge weights
vary from step to step in accord with the current partition.
Swap algorithm: finding the optimal move: Figure below exemplifies a graph Gαβ = [Nαβ; E{αβ] for finding the optimal swap move for a set of pixels Rαβ = Rα ∪ Rβ with the labels α and β:
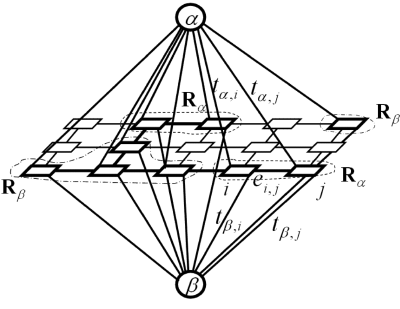
If the edges have the following weights:
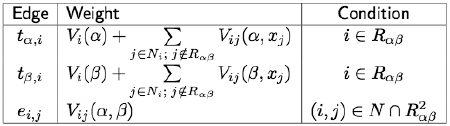
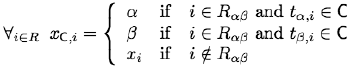
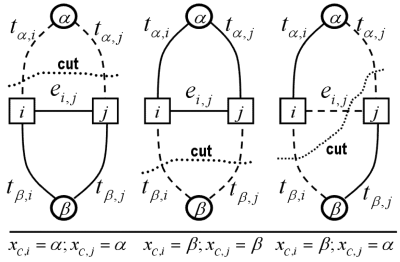
Each labelling xC corresponding to a cut C on the graph Gαβ is one α-β-swap away from the initial labelling x.
Because a cut separates a subset of pixels in Rαβ associated with one terminal from a complementary subset of pixels associated with another terminal, it includes (i.e. severs in the graph) an n-link ei,j between the neighbouring pixels in Rαβ if and only if the pixels i and j are connected to different terminals under this cut:
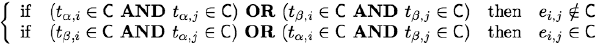
Theorem BVZ-T1 [Boykov, Veksler, Zabih, 2001]: There is an one-to-one correspondence between cuts C on Gαβ and labellings xC that are one α-β swap from x. The capacity of a cut C on Gαβ is c(C) = E(xC) plus a constant where E(…) is the energy function in Eq.(E1).
Corollary BVZ-C1
[Boykov, Veksler, Zabih, 2001]: The lowest energy labelling within a single
α-β-swap move from
a current labelling x is the labelling
![]() =
x°C corresponding to
the minimum cut
C° on
Gαβ.
=
x°C corresponding to
the minimum cut
C° on
Gαβ.
Expansion algorithm: finding the optimal move: The set of nodes Nα of the graph Gα = [Nα; Eα] for finding an optimal expansion-move includes the two terminals, denoted α and α, all the pixels i ∈ R, and a set of auxiliary nodes for each pair of the neighbouring nodes (i,j) ∈ E such that have different labels xi ≠ xj in the current partition P. The auxiliary nodes are on the boundaries between the partition sets Rλ; λ ∈ L. Thus the set of nodes is
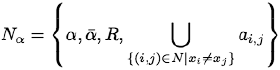
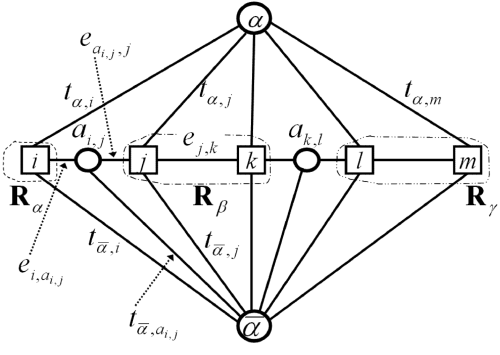
Each pixel i ∈ R is connected to the terminals α and α by t-links tα,i and t α,i, respectively. Each pair of the neighboring nodes (i,j) ⊂ N that are not separated in the current partition, i.e. have the same labels xi = xj in the current labelling, is connected with an n-link ei,j. For each pair of the separated neighboring pixels (i,j) ∈ N such that xi ≠ xj, the introduced auxiliary node ai,j results in three edges Ei,j = {ei, ai,j, eai,j ,j, t α,ai,j} where the first pair of n-links e… connects the pixels i and j to the auxiliary node ai,j, and the t-link connects the auxiliary node ai,j to the terminal α. Therefore, the set of all edges Eα is
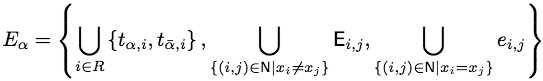
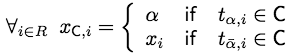
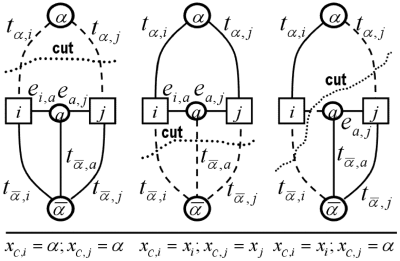
Each labelling xC corresponding to a cut C on the graph Gα is one α-expansion away from the initial labelling x.
Because a cut separates a subset of pixels in R associated with one terminal from a complementary subset of pixels associated with another terminal, it severs an n-link ei,j between the neighboring pixels (i,j) ∈ N if and only if the pixels i and j are connected to different terminals under this cut, or in formal terms:
(P1)
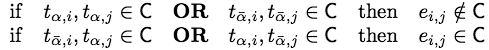
The triplet of edges Ei,j corresponding to a pair of neighboring pixels (i,j) ∈ N such that xi ≠ xj may be cut in different ways even when the pair of severed t-links at i and j are fixed. However, a minimum cut defines uniquely the edges to sever in Ei,j in these cases due to the minimality of the cut and the metric properties of the potentials associated with the edges {ei,ai,j, eai,j,j, tα,ai,j} ∈ Ei,j. The triangle inequality suggests that it is always better to cut any one of them, rather than the other two together. This property of a minimum cut C illustrated in above Figure MC has the following formal representation: if (i,j) ∈ C and xi ≠ xj, then C satisfies the conditions
(P2)

These properties may hold for non-minimal cuts, too. If an elementary cut
is defined as a cut satisfying the above conditions P1 and P2,
then it is possible to prove
Theorem BVZ-T2 [Boykov, Veksler, Zabih, 2001]: Let a graph Gα be constructed as above given a labelling x and α. Then, there is an one-to-one correspondence between elementary cuts on Gα and labellings within one α-expansion from x. The capacity of any elementary cut C is c(C) = E(xC) where E(…) is the energy of Eq.(E1).
Corollary BVZ-C2
[Boykov, Veksler, Zabih, 2001]:
The lowest energy labelling within a single α-expansion move from
x is the labelling
![]() =
xC° corresponding to
the minimum cut C° on
Gα.
=
xC° corresponding to
the minimum cut C° on
Gα.
Return to the local table of contents
Return to the global table of contents
Although the swap move algorithm has a wider application area due to only semimetric requirements to potentials Vi,j(…), generally it possesses no proven optimality properties. But a local minimum obtained with the expansion move algorithm is within a fixed factor of the global minimum, according to
Theorem BVZ-T3
[Boykov, Veksler, Zabih, 2001]:
Let ![]() be a labelling
for a local energy minimum when the expansion moves are allowed,
and let x* be the globally optimal solution.
Then,
be a labelling
for a local energy minimum when the expansion moves are allowed,
and let x* be the globally optimal solution.
Then, 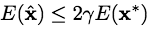 where
where
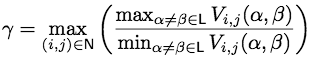
Proof:
Let some α ∈ L be fixed and let
R*α = {i ∈
R | x*i = α}.
Let xα be a labelling within one
α-expansion move from ![]() such that
such that
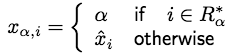
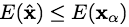 .
.
Let S = Spix ∪ Spair be an union of an arbitrary subset Spix of pixels in R; Spix ⊆ R, and of an arbitrary subset Spair of neighbouring pixels in N; Spair ⊆ N. A restriction of the energy of labelling x to S is defined as
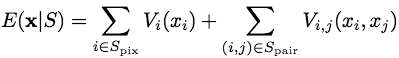
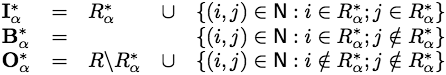
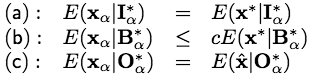
The union I*α ∪ B*α ∪ Oα includes all the pixels in R and all the neighbouring pairs of pixels in N. Therefore, Eq.(E2) can be rewritten as
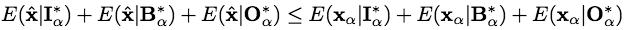
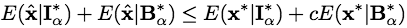
(E3)
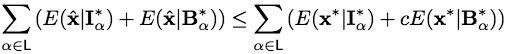
For every (i,j) ∈ B =
∪α∈L
B*α,
the term 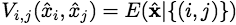 appears
twice on the left side of Eq.(E3): once in
appears
twice on the left side of Eq.(E3): once in
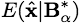 for α = x*i, and
once in
for α = x*i, and
once in 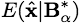 for α = x*j.
Similarly, every
for α = x*j.
Similarly, every
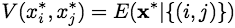 appears
2c times on the right side of Eq.(E3). Therefore, Eq.(E3)
can be rewritten as
appears
2c times on the right side of Eq.(E3). Therefore, Eq.(E3)
can be rewritten as
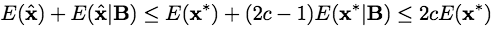
Pictures below taken from the Middlebury Stereo Vision Page http://www.middlebury.edu/stereo (see: D.Scharstein and R.Szeliski, "A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms", Int. J. Computer Vision, vol.47 (1/2/3), pp.7-42, April-June 2002) show that the graph-cut stereo algorithm notably outperforms both the dynamic programming stereo and the SSD-based stereo algorithms (this graph-cut algorithm of V.Kolmogorov and R.Zabih takes account of both matches and occlusions; see "Computing Visual Correspondence with Occlusions using Graph Cuts", Proc. 8th IEEE Int. Conf. on Computer Vision, Vancouver, Canada, July 9-12, 2001, vol.2, pp.508-515, 2001):

| 
| 
|
| Stereo pair "Tsukuba" | True disparity map | |
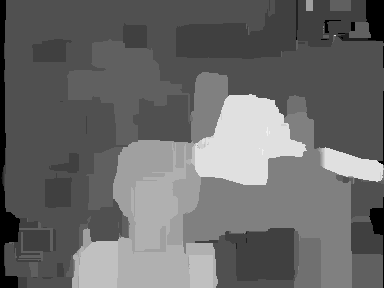
| 
| 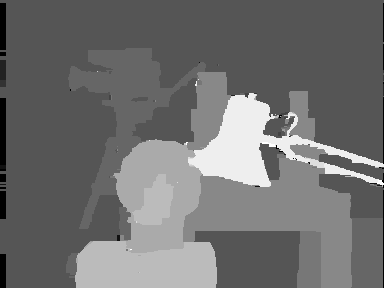
|
| SSD stereo (window 21×21) | Dynamic programming stereo | Graph-cut stereo |
| Grey-coded reconstructed disparity maps | ||
| 
| 
|
| Grey-coded signed disparity errors w.r.t. the true disparity map | ||