
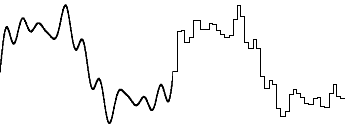
Figure 1. Analogue waveform to digital waveform conversion.
Take an audio wave for example. It's one-dimensional and varies over time. If this audio wave is sampled at a standard (CD) rate of 44.1 thousand samples per second, with each sample being an 8 bit value (0-255 range), a digital representation wave form is built up. Each sample explicitly records the amplitude of the wave at a point in time for 1/44,100th of a second. The resulting sequence of numbers is a digital representation of the original waveform.

Figure 1. Analogue waveform to digital waveform conversion.
To re-create the original waveform, the samples are simply played back in the correct order and at the correct speed. In the music/audio industry, this sort of encoding is referred to as Pulse Code Modulation (PCM). Why don't they just call it a digital sampling like everyone else? I don't know. Why is "floppy disk" spelt with a "k" and "compact disc" spelt with a "c"?
Obviously, when spatially encoding a waveform, the higher the sampling frequency and the greater the number of bits available to each sample value, then the higher the digitised wave quality will be.
To put that all another way, a spatial encoding function f(x) returns a result for each unique x value (x measuring time or space). A spectral encoding function g(u) returns a result for each unique frequency value, u.
A classic example of using sine waves to create non sine-like waveforms is in the approximation of a square wave (just about the most different waveform you can get from a sine wave).
By evaluating the sum below, a square-like wave can be produced:
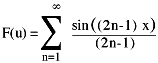

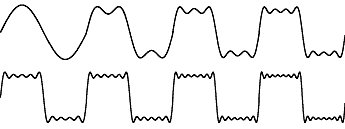
Figure 2. Square wave construction using sinusoids.
Notice how the sine wave becomes quite square after only a few iterations. Successive waves added after the 6th sine wave have significantly less effect on the waveform. This is an important effect and can be exploited for compression purposes (see the module on JPEG compression). To produce a near perfect square wave in this way would require an extremely large number of sine waves.
Take the audio waveform used in the first section again. The wave can actually be made up by adding five sine wave of various frequency and amplitudes together. Convenient, huh? Yes, it's one I prepared earlier. So instead of recording the power of a sample at a point in time, we can just record the frequency and amplitude of each sine wave. If the frequencies increase in a regular fashion then only the amplitudes need to be recorded.


Figure 3. Waveform construction using sinusoids.
To re-create the original waveform, simply add together all the sine waves of the correct frequency and amplitude. That's the easy part. Figuring out what each of the amplitudes need to be is the tricky bit. To discover this, it's time for some maths.
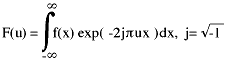
The inverse equation for spectral to spatial conversion is:
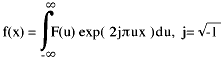
To illustrate these in action, a simple constant function f(x) and a graph of the power of its spectral equivalent F(u) is given below:
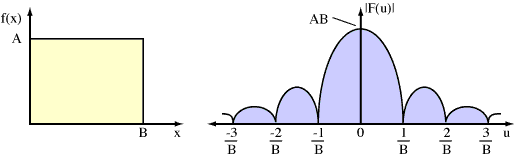
Figure 4. f(x) to F(u) function mapping.
Interesting? Yes, if you happen to like this sort of thing. Practical? Hmm, not really. To use it, you must know f(x), or mathematically model the input function f(x). Then some integration is required to find F(u) - not something that computers can do relatively quickly and efficiently.
The encoding (DFT) and decoding (inverse DFT) equations are:
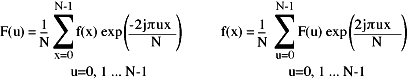
The integration required to do the Fourier Transform has now become a simple summation - something that computers can easily do.
A sampled waveform f(x) (the same as used previously) and its discrete spectral equivalent F(u) is given below:
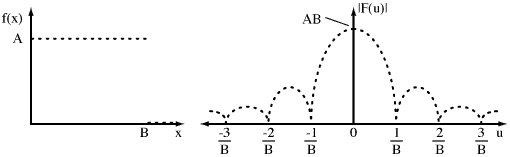
Figure 5. Discrete f(x) to F(u) mapping.
We're on the final leg now. There is just one awkward item left in the equations and that is the nasty square root of -1 (the j in the equation), which is of course an imaginary number. By making use of cosines we can construct the waveform using simple arithmetic.
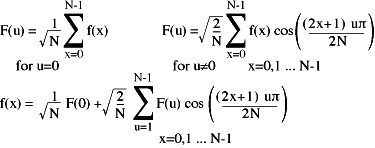
OK, so the equations look bigger - but really there's nothing complicated in there. We're just adding up square roots and cosines and things.
The frequency coefficients, F(u), are generated in order of increasing frequency, which is handy. Other than being a good form for compression, spectral space is a handy way of applying some filters to waveforms. For example, high, low and band-pass filters are ridiculously easy to implement - simply drop the F(u) coefficients which fall within the filter frequencies.
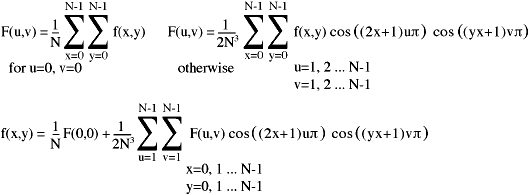
The final example in this module is a scanned image (32 x 32 pixels in size) which has been DCT encoded. The resulting frequency coefficients start with the low frequency values in the top left-hand corner and run to the high frequency values in the bottom right. The top left pixel is actually a scaled average of the whole image and is usually referred to as the DC component (as in AC/DC. Alternating currents vary over time, whereas DC currents don't - or rather, shouldn't).

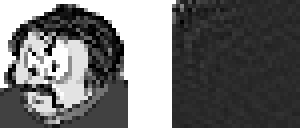
Figure 6. Original 2-D image and scaled DCT coefficients.
Those of you who have looked at what the DCT equations are actually doing, may well have noticed that the output from the DCTs are real numbers. In fact the range of these values is dependent on the size of the image being converted. The coefficients in figure 6 have been cunningly scaled down to a [0..255] range.
The most important thing to notice at this stage is that the contrast of the DCT coefficient image is much lower than the original image, with most of the important information being contained in the low frequency components.
There are some questions you can try to answer
on spatial and spectral encoding.
How did you find this 'lecture'? Was it too hard? Too easy? Were there something in particular you would like graphically illustrated? If you have any sensible comments, email me and let me know.
References: