The use of object shape is one of the most challenging problems in creating efficient CBIR. The object's shape plays a critical role in searching for similar image objects (e.g. texts or trademarks in binary images or specific boundaries of target objects in aerial or space images, etc.). In image retrieval, one expects that the shape description is invariant to scaling, rotation, and translation of the object and is naturally either 2D or 3D depending on the object.
Shape features are less developed than their colour and texture counterparts because of the inherent complexity of representing shapes. In particular, image regions occupied by an object have to be found in order to describe its shape, and a number of known segmentation techniques combine the detection of low-level colour and texture features with region-growing or split-and-merge processes. But generally it is hardly possible to precisely segment an image into meaningful regions using low-level features due to the variety of possible projections of a 3D object into 2D shapes, the complexity of each individual object shape, the presence of shadows, occlusions, non-uniform illumination, varying surface reflectivity, and so on (Castelli & Bergman, 2002).
After segmenting objects, their shapes have to be described, indexed, and compared. However no mathematical description is able to fully capture all aspects of visually perceived shapes as well as shape comparison is also a very difficult problem. The elusive nature of shape hinders any formal analysis of a trade-off between the complexity of shape description and its ability to describe and compare shapes of interest. At present CBIR exploits two large groups of 2D shape descriptors, namely, contour-based and region-based, representing either an outer boundary (or contour) or an entire region. These representations can also be combined together.
Both boundary-based and region-based descriptions are perceptually meaningful and interchangeable in the sense that each one can be used as a basis to compute the other (e.g. by filling-in the interior region or by tracing the boundary). But the explicit shape features available in each type of description are quite different, so that an ideal description should include both boundaries and regions in order to obtain more efficient retrieval.
Boundary representation describes the closed curve surrounding the
shape. The curve can be specified in numerous ways, e.g., by chain
codes, polygons, circular arcs, splines, or boundary Fourier descriptors:
Let, for example, the 1D boundary template be modelled, by a second-order spline parametrised by arc length. The template deforms to match a sketch in an "elastic" way, by maximising the edge strength integral along the curve while minimising the strain and bending energies modelled by integrals of the first and second derivatives of the deformation along the curve. Shape similarity is measured by combining the strain and bending energy, edge strength along the curve, and curve complexity (Castelli & Bergman, 2002).
Curvature of planar curves is one of the most powerful tools for representing and interpreting objects in an image. Although curvature extraction from a digitized object contour would seem to be a rather simple task, few methods exist that are at the same time easy to implement, fast, and reliable in the presence of noise. (Leymarie & Levine). Important features of an object's boundary related to the curvature function are extrema or peaks of curvature, points of inflection (i.e., zero-crossings of curvature), and segments of constant curvature that correspond to straight line segments or circular arcs of the boundary.
Let c(t) = (x(t), y(t))
and c(x, y) = 0 present an explicit (with two Cartesian parametric equations)
and implicit definitions of the same planar curve, respectively. The curvature k in
each point of the curve measures the curve's bending, i.e. the speed of changing of
the angle between the tangent vector to the curve and the x-axis. Let s
and φ denote the arc length along the curve and the tangential angle, respectively.
It is shown in differential geometry that:
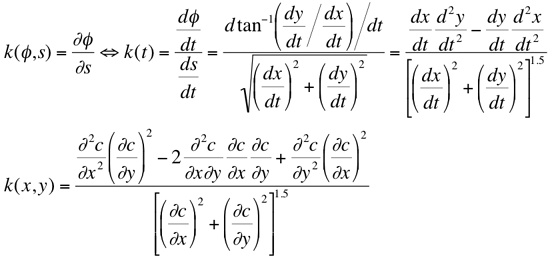
Region-based, or interior descriptions of shape specify the object's "body" within the closed boundary. Such a shape is represented with moment invariants, or a collection of primitives such as rectangles, disks, quadrics, etc., deformable templates, skeletons, or simply a set of points.
A skeleton represents each shape with the axis of symmetry between a pair of boundaries. The simplest skeleton is given by the medial axis defined as the trace of a locus of inscribed maximum-size circles. The skeleton is usually represented by a graph.
A shock set created by propagation from boundaries (similar to a "grassfire" initiated from the boundaries) is another variant of the medial axis. Shocks are singularities formed from the collisions of propagating fronts. By adding shock dynamics to each point and grouping the monotonically flowing shocks into branches, a shock graph is formed. Comparing to the skeletal one, the shock graph results in a finer partition of the medial axis.
Because shape is also defined in terms of presence and distribution of oriented parts, the quantitative characteristics of objects' orientation within an image, for instance, angular spectra of image components or edge directionality, may serve as global shape descriptors. In particular, the blobworld model efficiently describes objects separated from the background by replacing each object with a "blob", or an ellipse identified by the centroid and the scatter matrix. The blob is characterised also with the mean texture and the two dominant colours. The initial images are segmented using an Expectation - Maximisation (EM) algorithm based on colour and texture features.
Shape features include also spatial relationships of objects, in particular, topological and directional relationships. The first group describes the relations between object boundaries, such as "near to", "within", or "adjacent to". The second group shows the relative positions of objects with respect to each other, e.g. "in front of", "on the left of", or "on top of". Such spatial relationships are frequently described with the attributed-relational graph (ARG). Nodes of the graph represent objects, and an arc between two nodes represents a certain relationship between them.
That shape often carries semantic information follows from the fact that
many characteristic objects can be visually recognised solely from their
shapes. This distinguishes shape from other elementary visual features such as
colour, motion, or texture. The latter are equally important, but do not
identify an object (Bober, 2001; Sikora, 2001).
But the notion of object shape has many meanings. To deal with 3D real-world
objects, MPEG-7 standard has a 3D shape descriptor. The use of only 2D projections
of 3D objects onto an image plane lead to notions of region- and contour-based
similarity outlined below:
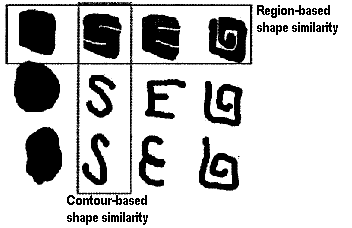
MPEG-7 supports both botions of similarity using region-based and contour-based shape descriptors. When a 3D object model is unknown but a set of 2D views specifies jointly the 3D properties of the object, MPEG-=7 provides a 2D/3D shape descriptor. Because the reconstruction of the original shape from the description is not required, the MPEG-7 descriptors are very compact. Also they are invariant to scaling, rotation, translation, and to some shape distortions due to imaging conditions (e.g. a perspective transformation under changing angle of view), non-rigid object deformations, or distortions resulting from image segmentation or shape extraction processes.
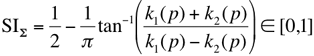
The principal curvatures are the eigenvalues of the local Hessian matrix H(p)
at point p. Provided that z = Σ(x,y) is a 3D surface
over the coordinate (x,y)-plane, the Hessian at point
p = (x,y,z) is the symmetric 2×2 matrix
of second derivatives:
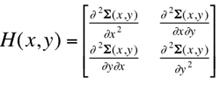
Shape spectrum is the histogram of the shape index values over the entire 3D surface. For 3D meshes, the shape index is computed for each vertex of the mesh. The spectrum is invariant to scaling, rotation, and translation. The default descriptor has histogram with 100 bins, 12 bit per bin. The descriptor has two additional variables: (i) the relative area of planar surface regions in the mesh, with respect to the entire area of the 3D mesh, and (ii) the relative area of all polygonal components where the shape index cannot be reliably estimated with respect to the entire area of the 3D mesh.
The region-based shape descriptor uses region moments which are invariant to transformations as the shape feature. It can describe complex objects with multiple disconnected regions as well as simple objects with or without holes (Bober, 2001; Sikora, 2001), gives a compact description of multiple disjoint regions simultaneously, allows for splitting of an object during segmentation into disconnected sub-regions, providing the information which regions it was split into is retained, and is robust to segmentation noise (e.g. salt-and-pepper noise).
The descriptor uses a complex-valued Angular Radial Transformation (ART) defined on a unit
disk in polar coordinates with a set of ART basis functions
Vmn(ρ, θ) of order n and m that are separable along the
angular and radial directions:
| 
| 
| 
| 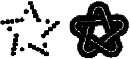
|
| (A) | (B) | (C) | (D) | (E) |
The contour-based shape descriptor is based on the curvature scale-space (CSS) representation of the contour (Mokhtarian & Mackworth, 1992 If an object contains several disjoint regions, each region has a separate contour-based shape description. A CSS index for matching shapes indicates the height of the most prominent peak and the horizontal and vertical positions of the remaining peaks in a specific CSS "image" describing a contour shape. The descriptor includes the eccentricity and circularity values of the original and filtered contours (6 bits each), the number of peaks in the CSS image (6 bits), the height of the highest peak (7 bits), and the x and y positions of the remaining peaks (9 bits per peak). The average size of the descriptor is 112 bits per contour
This descriptor
is efficient for describing objects for which characteristic shape features
are contained in the contour (e.g. the shapes in set A below) or objects
having similar region but very different contour
properties (the set B below);

| 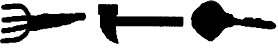
| |
| (A) | (B) | |

| 
| 
|
| (C) | (D) | (E) |
The descriptor has been selected on the basis of comprehensive comparative tests performed by the MPEG team. These tests have shown that the CSS outperforms most popular other approaches, including Fourier-based shape description techniques, shape representations based on Zernike moments or turning angles, and wavelet-based techniques
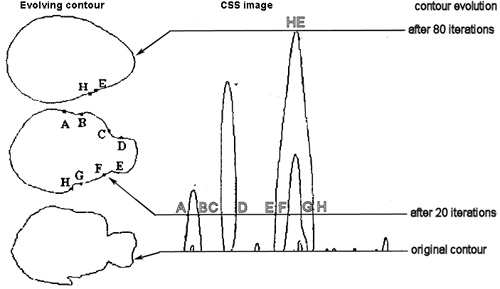
To form a CSS description of a contour, N equi-distant points {(xi,yi): i = 1, ..., N} are selected on the contour, starting from an arbitrary point 1 on the contour and following the contour clockwise. The contour is gradually smoothed by repetitive application of a low-pass moving filter (0.25, 0.50, 0.25) to two series X = {x1, x1, ..., xN} and X = {x1, x1, ..., xN} of the individual x and y coordinates of the selected N contour points. During the smoothing, the contour evolves. Its concavities are gradually flatten-out until the contour becomes convex (see also the SQUID retrieval system developed under supervision of Prof. J. Kittler and Dr. F. Mokhtarian which uses the CSS shape representation and shape-based queries).
The contour evolution can be illustrated using a special CSS "image"
associated with the evolutionary process (it need not be explicitly formed but is
convenient to demonstrate the CSS representation). Horizontal coordinates xcss
of the CSS
image correspond to the N indices of the selected contour points that
represent the contour. Vertical coordinates ycss
of the CSS image correspond to the number of
iterations of smoothing applied to the coordinate sets X and Y:
The shape of a 3D object can be approximately represented with a limited number of 2D shapes taken from different viewing directions. The 2D/3D shape descriptor forms a complete 3D view-based representation of the object by combining 2D descriptors representing its visible 3D shape seen from different view angles. Generally, any 2D visual descriptor, e.g. contour shape, region shape, colour, or texture, can be used. The 2D/3D descriptor allows for integrating the 2D descriptors used in the image plane to describe features of real-world 3D objects. Then a similarity matching between 3D objects is based on matching multiple corresponding pairs of 2D views of the objects.
Content-based visual information retrieval (CBIR) is based on extracting and indexing of metadata, objects and features, and relations between objects in images and video. Indexing pursues the goals to accelerate the queries and overcome the "curse of dimensionality" in performing the content-based search. Metadata indexing is a complex application-dependent problem that includes automatic analysis of unstructured text descriptions, definition of image standards and translation between different standards. But indexing of objects and features in multimedia databases is even more complex and difficult problem that has no general solution. For instance, descriptions of spatial relations in images are mostly developed in very special application domains such as modern geographic information systems (GIS).
Feature-level image representation reduces the QBE (query by image example) retrieval to computation of similarity between multidimensional feature vectors describing either a whole image or a portion of it. In the first case (whole image match) the query template is an entire image and the similar images have to be retrieved. A single feature vector is used for indexing and retrieval. Such matching was used in retrieving photographic images and adopted in early CBIR systems like QBIC.
In the second case (subimage match) the query template is a portion of an image, and the retrieval results in images with similar portions or just in portions of images containing desired objects. Such a partial matching is important for many application areas such as remotely sensed images of the Earth or medical images. Most today's CBIR systems support subimage retrieval by segmenting the stored images and associating a feature vector with each potentially interesting segment. The segmentation may be data-independent (a set of non-overlapping or overlapping rectangular regions called blocks or windows) or data-dependent (adaptive).
Today's CBIR involves different low-level colour, texture, and shape descriptors. Typically these descriptors are represented by multidimensional vectors, and similarity between two images is specified by some quantitative measure in the feature space. For the vector feature space, a range query results in retrieving all the points lying within a hyperrectangle aligned with the coordinate axes. But to support nearest-neighbour and within-distance (or A-cut) queries, the feature space must possess a metric or a dissimilarity measure. The same vector metrics can be used to define the dissimilarity between statistical distributions, although these latter have also specific dissimilarity measures. Most common dissimilarity / similarity measures are as follows:
Dissimilarity / similarity between two n-dimensional vectors
x and y
(the n×n matrix C is a covariance matrix for
a data set;
the matrix K is a positive definite but not necessarily a covariance matrix;
the bars denote average values of the vector components for the entire
the data set;
vector components in the relative entropy or chi-square distance are
positive.
The unit spheres under Chebyshev, Euclidean, and city-block distance.
The Chebyshev, Euclidean, and city-block distances are particular cases of the Minkowsky family of distances. All the Minkowsky distances differ in the way they combine the contributions of coordinate-wise differences di = xi - yi between the vectors x and y. When p = 1, all the absolute differences contribute equally to the distance D[1](x,y). When p grows, the value D[p](x,y) is increasingly determined by the maximum of the absolute differences,whereas the overall contribution of all the other differences becomes less and less significant.
A brute-force sequential scanning of the database is computationally infeasible. To search in large databases, indexing of the vectors and search keys that accelerates the retrieval becomes a must. Most popular indexing structures are based on representing the feature vectors as points in a multidimensional vector space and accounting for either particular regions in it (vector space indexes), or pairwise distances between the objects in a database (metric space indexes). From the algorithmic viewpoint, the indexing structures are nonhierachical, recursive, and projection based (Castelli & Bergman, 2002). Nonhierachical indexing divides the feature space into regions such that each region a query point belongs to is found in a fixed number of steps. Recursive indexing organised the space as a tree in order to optimise computational efficiency of the retrieval. Projection-based indexing tries to search on the linear or nonlinear projections of database points onto a subspace in the feature space. This latter method relates closely to reduction of dimensionality of the feature space for a given database.
Nonhierarchical indexing maps the n-dimensional vectors onto the real line using a space-filling curve (e.g., Peano or Hilbert one). The mapped records are indexed with a 1D indexing structure. Because space-filling curves preserve to some extent the neighbourhood relations between initial vectors, range queries, nearest-neighbour queries, and A-cut queries are approximated rather closely along the linear mapping.
Recursive indexing divides recursively the search space into successively smaller regions that depend on the data set being indexed. The resulting decomposition of the space is well-represented by a tree. The most popular trees in recursive indexing are quad-trees, k-n-trees and R-trees. Quad-trees in the n-dimensional space are trees of degree 2n, so that each nonterminal node has 2n children. Each nonterminal node of a n-quad-tree divides the n-dimensional space into 2n hyperrectangles aligned with the coordinate axes. The partitioning is obtained by simultaneously splitting each coordinate axis into two parts. K-n-trees divide the space with (n-1)-dimensional hyperplanes perpendicular to a specific coordinate axis selected as a function of the data related to the node. Each nonterminal node has at least two children.
R-trees generalise multiway B-trees allowing, with a scalar search key, an extremely efficient search. For multidimensional indexing, the R-tree and its modifications are the best (Castelli & Bergman, 2002). The R-tree is a B-tree-like indexing structure where each internal node represents a k-dimensional hyperrectangle rather than a scalar range. The hyperrectangle of the node contains all the hyperrectangles of the children. The rectangles can overlap, so that more than one subtree under a node may have to be visited during a search. To improve a performance, the R*-tree is proposed that minimises the overlap among the nodes.
Multiway search R-tree: a vector search key is compared to the hyperrectangles in each successive node.
But both R-trees and R*-trees work well until the dimension of the indexing key is less than 20. Otherwise dimension reduction should be performed before indexing the feature vectors. The main problem is that our three-dimensional geometric intuition fails when the number of dimensions grows, e.g., almost all the volume of a 100-dimensional hypercube is outside the largest inscribed sphere:
Ratio between the volumes of the minimum bounding hypercube and the hypersphere
Another difficulty caused by the "curse of dimensionality" is that the high-dimensional vector spaces demonstrate no tightly concentrated clusters of data items typical to the low-dimensional cases. Let us consider a simple example: n-dimensional feature vectors x=[x1, ..., xn] with independent components having each the standard normal (Gaussian) distribution with zero mean and the standard deviation s. The Euclidean distance d between the two independent vectors x and y of that type is defined as follows
Therefore, the mathematical expectation and the variance of the square distance are 2ns2 and 4ns4, respectively. If s = 1, then in the one-dimensional (1D) case with n = 1, the square distance between the two features is distributed asymmetrically around the value 2 with the standard deviation equal to 2 so that a vast majority of the distances d are within the range [0, 2.8]. But in the 100-dimensional case (n = 100) the distribution is almost symmetrical around 200 with the approximate standard deviation 20. Thus most of the distances d are within the range [11.4, 16.1], and there are no points "close" to or "far" from the query. It is evident that in the multi-dimensional case the nearest-neighbour or within-distance (A-cut) queries become essentially meaningless.
Fortunately, in practice the feature space has often a local structure that makes the notion of close neighbourhood of a query image still meaningful. Also, the features are usually interdependent and can be well-approximated by their projections onto an appropriate lower-dimensional space, where the distance- or similarity-based indexing behaves well. The mapping from a higher-dimensional to a lower-dimensional space is called dimensionality reduction and performed by selecting a subset of variables (possibly after a linear transformation of the feature space), or multidimensional scaling, or geometric hashing (Castelli & Bergman, 2002).
Selection of a subset of variables reduces the dimensionality of the feature space by discarding "less characteristic" dimensions. These methods are popular in applied statistics and pursue the goal of minimising the error of approximation of the original vectors with lower-dimensional projections after a linear transformation of the feature space. The transformation makes the transformed features uncorrelated, that is, the covariance matrix of the transformed data set becomes diagonal. This method is known under different names, for instance, the Karhunen-Loeve transform (KLT), principal component analysis (PCA), or singular value decomposition (SVD). Although particular numerical algorithms may differ, all the above methods are equivalent in essence. The choice of variables is governed by the scatter (variance) of the data set around each new coordinate axis, the chosen subset of variables having usually to preserve a given percentage (e.g., 95% or 99%) of the total scatter of the original data set. This approach minimises the mean squared error of discarding each particular number of dimensions with smaller variance, so that the original vectors are closer in Euclidean distance to their decorrelated projections than with any other linear transformation. But the approach is data-dependent, computationally expensive, and suited well for only static databases. Dynamic databases with regularly inserted and deleted items need special (and usually computationally very expensive) techniques for effectively updating the KLT/PCA/SVD of a data set.
Principal component analysis (PCA) performs linear transformation of
a number of possibly
correlated feature vectors into a possibly smaller number of uncorrelated
vectors called principal components. The first principal component accounts
for the maximal variability in the feature vectors projected onto this line, and each
next component accounts for the maximal remaining variability in the feature space.
Let
fk; k = 1, ..., K, denote given
n-dimensional vectors with the empirical mean m and the
empirical covariance matrix S:
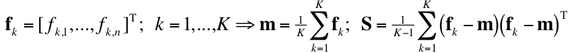
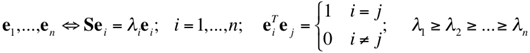
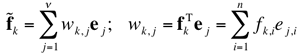
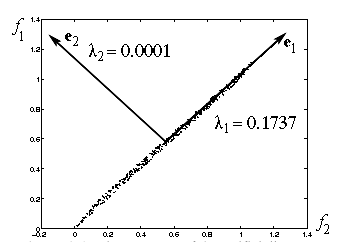
Multidimensional scaling is based on nonlinear mapping of the n-dimensional feature space into m-dimensional one (m < n). There is no general theory or precise definition of this approach. In many cases the metric multidimensial scaling tries to minimise changes of the pairwise Euclidean distances between the objects in a data set, but numerous other statements of the problem exist. In general, nonlinear mapping can provide better dimensionality reduction than linear methods, but at the expense of much heavier computations. The approach is also data-dependent and poorly suited for dynamic databases.
Geometric hashing performs data-independent mapping of the n-dimensional feature space into a very low-dimensional one, namely, the 1D real line or the 2D real plane. Ideally, hashing spreads the database uniformly across the range of the low-dimensional space, so that the metric properties of the hashed space differ significantly from those of the original feature space. This is why geometric hashing is applied to indexing of low-dimensional feature spaces in the case when only their local metric properties need to be maintained. Also, the difficulties in designing a good hashing function grow with the dimensionality of the original space.
Generally, dimensionality reduction facilitates efficient indexing of multidimensional feature spaces, but the search is now performed on the transformed rather than original data. But in many cases the approximation reduces impacts of the "curse of dimensionality" and improves the retrieval. If only a particular class of queries has to be supported, more efficient multidimensional indexing structures can be developed. In particular, to capture the local structure of a database without involving computationally expensive multidimensional scaling, CSVD (Clustering with Singular Value Decomposition), proposed by Thomasian, Castelli, and Li, first partitions the data into homogeneous clusters and then separately reduces the dimensionality of each cluster. The number of the clusters is selected empirically, and the index is represented as a tree, each node containing the cluster parameters (the centroid and radius) and the dimensionality reduction information (the projection matrix and the number of retained dimensions). Nonleaf nodes contain information for assigning a query vector to its cluster and pointers to the children, each of which represents a separate cluster. Terminal nodes (leaves) contain an indexing scheme supporting nearest-neighbour queries.